Câu hỏi:
2 năm trước
Cho hàm số y=f(x) xác định là liên tục trên R có đạo hàm f′(x)=(x−2)(x+5)(x+1) và f(2)=1. Khi đó số điểm cực trị của hàm số g(x)=[f(x2)]2 là
Chỉ được điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
Từ giả thiết ta có: f′(x)=0⇔[x=2x=−5x=−1
Bảng biến thiên của y=f(x)
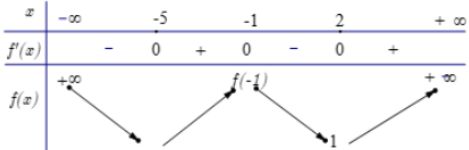
Từ BBT suy ra f(x)>0∀x≥0 nên f(x2)>0∀x∈R
Xét hàm số g(x)=[f(x2)]2 ta có:
g′(x)=2.[f(x2)]′.f(x2)=2.2x.f′(x2)f(x2)=4x.f(x2).f′(x2)
=4x.(x2−2).(x2+5)(x2+1)f(x2)
g′(x)=0⇔[x=0x=√2x=−√2
Bảng biến thiên của g(x):
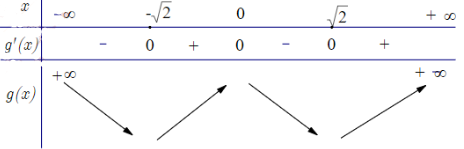
Từ bảng biến thiên trên ta được hàm số g(x) có 3 điểm cực trị.
Hướng dẫn giải:
- Giải phương trình f′(x)=0
- Lập bảng biến thiên của y=f(x)
- Lập bảng biến thiên của g(x)

 (Nguồn: ourwordindata.org)
(Nguồn: ourwordindata.org)