Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?

Ta có:

\(g'\left( x \right)  = \left[ {f\left( {1 - x} \right)} \right]' = \left( {1 - x} \right)'f'\left( {1 - x} \right)=  - f'\left( {1 - x} \right)\)

\(=  - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\) \( =  - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\)

Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)

\( \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\)

\( \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\) (do \(x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)\))

\( \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge  - m\,\,\forall x \in \left( { - \infty ; - 1} \right)\)

\(\Leftrightarrow  - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)\).

Ta có \(h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x =  - 2\).

BBT:

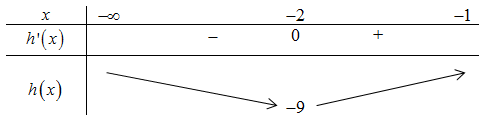
Dựa vào BBT ta có \( - m \le  - 9 \Leftrightarrow m \ge 9\).

Mà \(m \in \left[ { - 2019;2019} \right]\) và \(m\) nguyên nên \(m \in \left[ {9;10;11;...;2019} \right]\) hay có \(2019 - 9 + 1 = 2011\) giá trị của \(m\) thỏa mãn.