Câu hỏi:
3 năm trước
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình bên. Số điểm cực trị của hàm số đã cho là:
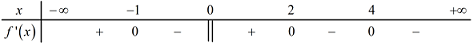
Trả lời bởi giáo viên
Đáp án đúng: d
Dựa vào bảng xét dấu ta thấy \(f'\left( x \right)\) đổi dấu qua \(x = - 1,\,\,\,x = 0\) và \(x = 2\) nên hàm số có 3 điểm cực trị.
Hướng dẫn giải:
Ta có: \(x = {x_0}\) là điểm cực trị của hàm số \(y = f\left( x \right) \Leftrightarrow \) tại điểm \(x = {x_0}\) thì hàm số có \(y'\) đổi dấu từ dương sang âm hoặc ngược lại.
Hay số điểm cực trị của hàm số là số lần đổi dấu của \(f'\left( x \right).\)


