Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ và diện tích hai phần A, B lần lượt bằng 11 và 2.

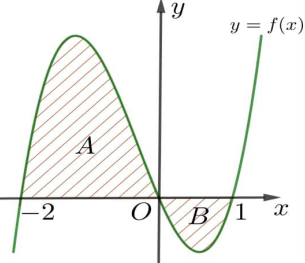
Tính giá trị của \(I = \int\limits_{ - 1}^0 {f\left( {3x + 1} \right)dx} \) bằng

Chỉ điền số nguyên, phân số dạng a/b

Đáp án:

Bạn Thư nhận công việc partime viết bài cho tòa soạn \(M\) và được trả lương theo quý. Quý đầu tiên tiền lương là 2 triệu đồng, kể từ quý thứ hai mức lương sẽ tăng thêm 500 nghìn đồng mỗi quý. Sau một năm số tiền bạn Thư nhận được từ công việc partime này là

Có 5 ứng cử viên xin việc, trong đó có 3 ứng cử viên có đơn xin việc được xếp loại \(A\). Giám đốc cần chọn ra 2 ửng cử viên. Xác suất để trong 2 ứng cử viên được chọn có đúng 1 ứng cử viên có đơn xin việc xếp loại A là:

Điền số nguyên hoặc phân số dạng a/b vào chỗ trống

Cho biểu đồ về sự tác động của một số thực phẩm tới môi trường:

(Nguồn: ourwordindata.org)

Thực phẩm nào tác động tới môi trường ít nhất?

Tìm tất cả các giá trị của tham số m để đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x + m - 2\) cắt trục hoành tại hai điểm phân biệt?

Cho bất phương trình: \(\dfrac{{\left| {x - 1} \right|}}{{x + 2}} > 1.\) Nghiệm nguyên lớn nhất của bất phương trình trên là: