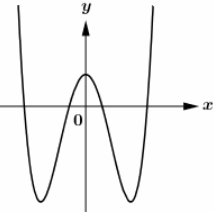
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
Tìm số điểm cực trị của hàm số \(F\left( x \right) = 3{f^4}\left( x \right) + 2{f^2}\left( x \right) + 5\)
Trả lời bởi giáo viên
TXĐ: \(D = \mathbb{R}\).
Ta có \(F\left( x \right) = 3{f^4}\left( x \right) + 2{f^2}\left( x \right) + 5\).
\(\begin{array}{l} \Rightarrow F'\left( x \right) = 12f'\left( x \right).{f^3}\left( x \right) + 4f'\left( x \right).f\left( x \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 4f'\left( x \right)f\left( x \right)\left[ {{f^2}\left( x \right) + 1} \right] = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 0\end{array} \right.\end{array}\)
Dựa vào đồ thị hàm số ta thấy:
Phương trình\(f'\left( x \right) = 0\) có 3 nghiệm đơn phân biệt.
Phương trình \(f\left( x \right) = 0\) có 4 nghiệm đơn phân biệt.
Rõ ràng cả 7 nghiệm này là phân biệt với nhau.
Vậy hàm số \(F\left( x \right)\) có tất cả 7 điểm cực trị.
Hướng dẫn giải:
- Tính đạo hàm của hàm số \(F\left( x \right)\).
- Giải phương trình \(F'\left( x \right) = 0\), xác định các nghiệm mà qua đó \(F'\left( x \right)\) đổi dấu.
Giải thích thêm:
Học sinh cẩn thận khi tính đạo hàm của hàm hợp.
Câu hỏi khác
(Nguồn: ourwordindata.org)- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
