Câu hỏi:
3 năm trước
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ.
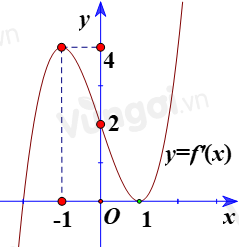
Số điểm cực trị của hàm số \(y = f\left( x \right) - 5x\) là
Chỉ được điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
Ta có: \(y' = f'\left( x \right) - 5\)
\(y' = 0 \Leftrightarrow f'\left( x \right) = 5\)
Số cực trị của hàm số bằng số nghiệm đơn của phương trình trên.
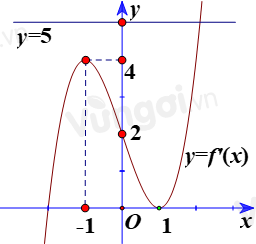
Dựa vào đồ thị ta có \(y = f'\left( x \right)\) cắt đường thẳng \(y = 5\) tại đúng 1 điểm \({x_0}\) (\({x_0}\) là nghiệm đơn của phương trình \(f'\left( x \right) = 5\)).
Vậy hàm số \(y = f\left( x \right) - 5x\) có đúng 1 điểm cực trị.
Hướng dẫn giải:
Xét số nghiệm của \(f'\left( x \right) - 5 = 0\) dựa vào đồ thị hàm số.


