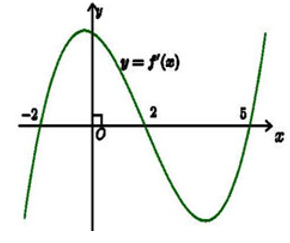
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục trên R và đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của \(m\) để hàm số \(y = f\left( {\left| {x + 1} \right| - m} \right)\) có 3 điểm cực trị. Tổng tất cả các phần tử của tập hợp \(S\) bằng ?
Trả lời bởi giáo viên
Hàm số \(y = f\left( x \right)\) có 3 điểm cực trị là \( - 2,\,\,2,\,\,5\).
Nên hàm số \(y = f\left( {\left( {x + 1} \right) - m} \right)\) có 3 điểm cực trị là \(\left[ \begin{array}{l}x + 1 - m = - 2\\x + 1 - m = 2\\x + 1 - m = 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = m - 3\\x = m + 1\\x = m + 4\end{array} \right.\)
Hàm số \(y = f\left( {\left( {|x + 1|} \right) - m} \right)\) có đúng 3 điểm cực trị khi \(y = f\left( {\left( {x + 1} \right) - m} \right)\) có đúng 1 cực trị lớn hơn \( - 1\).
Do đó \(\left\{ \begin{array}{l}m - 3 \le - 1\\m + 1 \le - 1\\m + 4 > - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 2\\m \le - 2\\m > - 5\end{array} \right. \Leftrightarrow - 5 < m \le - 2\). Mà \(m \in \mathbb{Z}\) \( \Rightarrow m \in \left\{ { - 4; - 3; - 2} \right\}\)
Vậy \(S = - 4 - 3 - 2 = - 9\).
Hướng dẫn giải:
Hàm số \(y = f\left( {\left| x \right|} \right)\) có \(2a + 1\) điểm cực trị khi hàm số \(y = f\left( x \right)\) có \(a\) điểm cực trị dương.
Câu hỏi khác
(Nguồn: ourwordindata.org)- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
