Câu hỏi:
2 năm trước
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
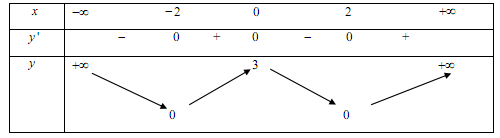
Khẳng định nào sau đây là khẳng định đúng:
Trả lời bởi giáo viên
Đáp án đúng: c
A, B sai vì hàm số chỉ nghịch biến trên các khoảng $\left( { - \infty ; - 2} \right)$ và $\left( {0;2} \right)$
D sai vì hàm số chỉ đồng biến trên khoảng $\left( { - 2;0} \right)$ và $\left( {2; + \infty } \right)$
C đúng vì giá trị thấp nhất của y trên bảng biến thiên là 0.
Hướng dẫn giải:
Quan sát bảng biến thiên và nhận xét các khoảng đồng biến, nghịch biến của hàm số và rút ra kết luận.
Định lý: Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $K$.
a) Nếu $f'\left( x \right) > 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ đồng biến trên $K$.
b) Nếu $f'\left( x \right) < 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ nghịch biến trên $K$.
Giải thích thêm:
Học sinh quan sát thấy chiều mũi tên đi lên từ $0$ đến $3$ chọn đáp án D là sai.
Một số em nhìn nhầm đáp án C thành $f'(x)\ge 0$ và kết luận không có đáp án đúng là sai, ở đây $f(x) \ge 0$ nghĩa là giá trị của hàm số luôn không âm (quan sát bảng biến thiên). Các em cần chú ý đọc kĩ đề bài.
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 đề số 2 Toán 12 có lời giải chi tiết
