Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
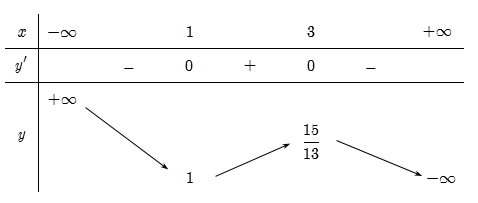
Biết $f\left( 0 \right) = \dfrac{7}{6}$, giá trị lớn nhất của \(m\) để phương trình \({e^{2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}}} = m\) có nghiệm trên đoạn \(\left[ {0;\,2} \right]\) là
Trả lời bởi giáo viên
Ta có: \({e^{2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}}} = m \Leftrightarrow 2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2} = \ln m\)
Xét \(g\left( x \right) = 2{f^3}\left( x \right) - \dfrac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \dfrac{3}{2}\) có:
\(g'\left( x \right) = 6{f^2}\left( x \right)f'\left( x \right) - 13f\left( x \right)f'\left( x \right) + 7f'\left( x \right) = f'\left( x \right)\left[ {6{f^2}\left( x \right) - 13f\left( x \right) + 7} \right]\)
Suy ra \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\6{f^2}\left( x \right) - 13f\left( x \right) + 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\f\left( x \right) = 1\\f\left( x \right) = \dfrac{7}{6}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1;x = 3\\x = 1,x = {x_1} > 3\\x = {x_2} < 1\end{array} \right.\)
Xét \(g\left( x \right)\) trên đoạn \(\left[ {0;2} \right]\).
+ Trong khoảng \(\left( {0;1} \right)\) thì \(f'\left( x \right) < 0,f\left( x \right) > 1,f\left( x \right) < f(0)=\dfrac{7}{6}\) nên \(f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \dfrac{7}{6}} \right) > 0\) hay \(g'\left( x \right) > 0\).
+ Trong khoảng \(\left( {1;2} \right)\) thì \(f'\left( x \right) > 0,f\left( x \right) > 1,f\left( x \right) <\dfrac{15}{13}< \dfrac{7}{6}\) nên \(f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \dfrac{7}{6}} \right) < 0\) hay \(g'\left( x \right) < 0\).
Từ đó ta có bảng biến thiên của \(g\left( x \right)\) như sau:
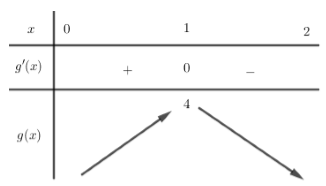
Từ bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = 4\).
Vậy yêu cầu bài toán thỏa nếu và chỉ nếu \(\ln m \le 4 \Leftrightarrow m \le {e^4}\) hay giá trị lớn nhất của \(m\) là \(m = {e^4}\).
Hướng dẫn giải:
- Lấy \(\ln \) hai vế rồi xét hàm số vế trái trên đoạn \(\left[ {0;2} \right]\).
- Tìm điều kiện để bài toán thỏa dựa vào tương giao đồ thị và suy ra giá trị \(m\).

