Cho hàm số \(y = 3\left| {x - 2} \right| - \left| {2x - 6} \right|\) có đồ thị \((C)\). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với \(x \in \left[ { - 3;4} \right]\)
Trả lời bởi giáo viên
Ta có \(y = \left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 3\\5x - 12\,\,\,\,khi\,\,2 < x < 3\\ - x\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 2\end{array} \right.\)
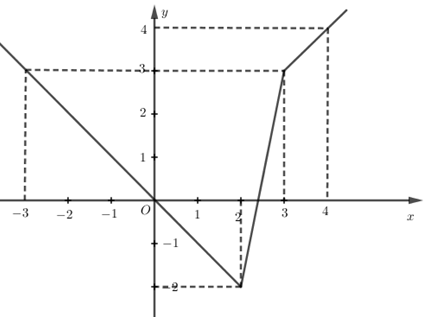
Vẽ đường thẳng \(y = x\) đi qua hai điểm \(O\left( {0;0} \right),\,\,A\left( {1;1} \right)\) và lấy phần đường thẳng bên phải của đường thẳng $x = 3$
Vẽ đường thẳng \(y = 5x - 12\) đi qua hai điểm \(B\left( {3;3} \right),\,\,C\left( {2; - 2} \right)\) và lấy phần đường thẳng nằm giữa của hai đường thẳng $x = 2,\,\,x = 3$.
Vẽ đường thẳng \(y = - x\) đi qua hai điểm \(O\left( {0;0} \right),\,\,D\left( { - 1; - 1} \right)\) và lấy phần đường thẳng bên trái của đường thẳng $x = 2$
Dựa vào đồ thị hàm số ta có:
\(\mathop {{\rm{max}}}\limits_{\left[ { - 3;4} \right]} y = 4\) khi và chỉ khi $x = 4$
\(\mathop {\min y}\limits_{\left[ { - 3;4} \right]} = - 2\) khi và chỉ khi $x = 2$
Hướng dẫn giải:
- Phá dấu giá trị tuyệt đối, vẽ đồ thị hàm số \(\left( C \right)\)
- Tìm GTLN, GTNN của hàm số trên \(\left[ { - 3;4} \right]\) và kết luận.

