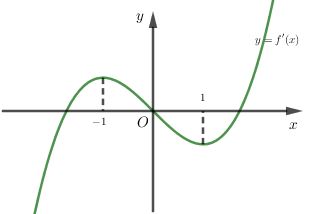
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 1 \right) = 1\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Có bao nhiêu số nguyên dương a để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - a} \right|\) nghịch biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\)?

Ta có:

\(\begin{array}{l}y = \left| {4f\left( {\sin x} \right) + \cos 2x - a} \right|\\y = \left| {4f\left( {\sin x} \right) + 1 - 2{{\sin }^2}x - a} \right|\end{array}\)

Đặt \(t = \sin x\), với \(x \in \left( {0;\dfrac{\pi }{2}} \right)\) thì \(t \in \left( {0;1} \right)\).

Khi đó hàm số trở thành \(y = \left| {4f\left( t \right) + 1 - 2{t^2} - a} \right| = \sqrt {{{\left[ {4f\left( t \right) + 1 - 2{t^2} - a} \right]}^2}} \).

Để hàm số nghịch biến trên \(\left( {0;1} \right)\) thì \(y' < 0\,\,\forall t \in \left( {0;1} \right)\).

\(\begin{array}{l}y' = \dfrac{{\left[ {4f'\left( t \right) - 4t} \right].\left[ {4f\left( t \right) + 1 - 2{t^2} - a} \right]}}{{\sqrt {{{\left[ {4f\left( t \right) + 1 - 2{t^2} - a} \right]}^2}} }} < 0\,\,\forall t \in \left( {0;1} \right)\\ \Leftrightarrow \left[ {f'\left( t \right) - t} \right].\left[ {4f\left( t \right) + 1 - 2{t^2} - a} \right] < 0\,\,\forall t \in \left( {0;1} \right)\,\,\left( * \right)\end{array}\)

Vẽ đồ thị hàm số \(y = f'\left( t \right)\) và \(y = t\) trên cùng mặt phẳng tọa độ ta có:

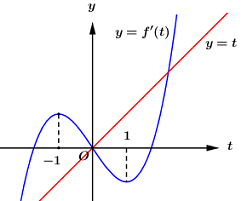
Dựa vào đồ thị hàm số ta thấy trên \(\left( {0;1} \right)\) đường thẳng \(y = t\) luôn nằm phía trên đồ thị hàm số \(y = f'\left( t \right)\), do đó \(f'\left( t \right) - t < 0\,\,\forall t \in \left( {0;1} \right)\).

\(\begin{array}{l}\left( * \right) \Leftrightarrow 4f\left( t \right) + 1 - 2{t^2} - a > 0\,\,\forall t \in \left( {0;1} \right)\\ \Leftrightarrow a < 4f\left( t \right) - 2{t^2} + 1\,\,\forall t \in \left( {0;1} \right)\end{array}\)

Đặt \(g\left( t \right) = 4f\left( t \right) - 2{t^2} + 1\), \(\forall t \in \left( {0;1} \right)\) \( \Rightarrow a \le \mathop {\min }\limits_{\left[ {0;1} \right]} g\left( t \right)\).

Ta có: \(g'\left( t \right) = 4f'\left( t \right) - 4t < 0\,\,\forall t \in \left( {0;1} \right)\).

\( \Rightarrow \) Hàm số \(g\left( t \right)\) nghịch biến trên \(\left( {0;1} \right)\), do đó \(\mathop {\min }\limits_{\left[ {0;1} \right]} g\left( t \right) = g\left( 1 \right) = 4f\left( 1 \right) - 1 = 3.\)

\( \Rightarrow a \le 3\). Mà a là số nguyên dương \( \Rightarrow a \in \left\{ {1;2;3} \right\}\).

Vậy có 3 giá trị của a thỏa mãn yêu cầu bài toán.