Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

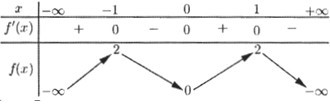
Số nghiệm thuộc đoạn \(\left[ {0;\dfrac{{5\pi }}{2}} \right]\) của phương trình \(f\left( {\sin \,x} \right) = 1\) là:

Xét \(x \in \left[ {0;\,\,\,\dfrac{{5\pi }}{2}} \right]:\) 

Đặt \(t = \sin x\,\,\,\,\left( {t \in \left[ { - 1;\,\,\,1} \right]} \right)\).

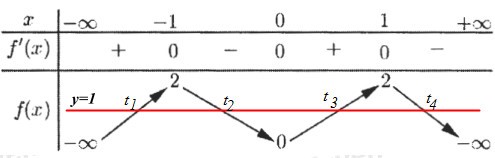
Dựa vào BBT ta thấy phương trình \(f\left( t \right) = 1\) có nghiệm \(\left[ \begin{array}{l}t = {t_1} <  - 1\,\,\,\,\left( {ktm} \right)\\t = {t_2} \in \left( { - 1;0} \right)\\t = {t_3} \in \left( {0;1} \right)\\t = {t_4} > 1\,\,\,\left( {ktm} \right)\end{array} \right.\)

Suy ra \(\left[ \begin{array}{l}\sin x = {t_2} \in \left( { - 1;0} \right)\\\sin x = {t_3} \in \left( {0;1} \right)\end{array} \right.\)

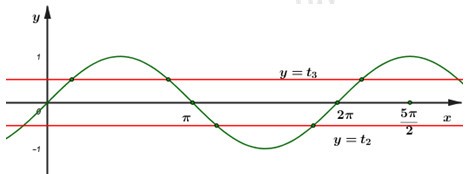
Dựa vào đồ thị hàm số ta thấy,

+) Phương trình \(\sin x = {t_3} \in \left( {0;1} \right)\) có 3 nghiệm trong đoạn \(\left[ {0;\dfrac{{5\pi }}{2}} \right]\)

+) Phương trình \(\sin x = {t_2} \in \left( { - 1;0} \right)\) có 2 nghiệm trong đoạn \(\left[ {0;\dfrac{{5\pi }}{2}} \right]\)

Vậy phương trình đã cho có tất cả 5 nghiệm trong đoạn \(\left[ {0;\dfrac{{5\pi }}{2}} \right].\)