Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).

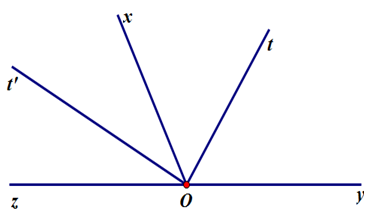
Vì tia \(Ot\) là phân giác \(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \dfrac{1}{2}\widehat {xOy}\) suy ra \(\widehat {xOy} = 2.\widehat {tOx}\) (1)

Và tia \(Ot'\) là phân giác \(\widehat {yOz}\) nên \(\widehat {zOt'} = \widehat {xOt'} = \dfrac{1}{2}\widehat {xOz}\) suy ra \(\widehat {xOz} = 2.\widehat {t'Ox}\) (2)

Mà \(\widehat {xOy};\,\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOz} = 180^\circ \) (3)

Từ (1) (2) (3) suy ra \(2.\widehat {tOx} + 2.\widehat {t'Ox} = 180^\circ \) suy ra \(2.\left( {\widehat {tOx} + \widehat {t'Ox}} \right) = 180^\circ  \Rightarrow \widehat {tOx} + \widehat {t'Ox} = 90^\circ \) (4)

Lại có  tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) và tia \(Ot'\) nằm giữa hai tia \(Ox;Oz\) nên tia \(Ox\) nằm giữa hai tia \(Ot;Ot'.\)

Do đó \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'}\) (5)

Từ (4) (5) suy ra \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'} = 90^\circ \).