Câu hỏi:
2 năm trước
Cho hai điện tích \(q_1 = 9.10^{ - 8}C\,;\,\,q_2 = - 16.10^{ - 8}C\) đặt tại hai điểm A, B trong không khí cách nhau \(12cm.\) Tìm điểm M tại đó có vecto cường độ điện trường bằng không.
Trả lời bởi giáo viên
Đáp án đúng: c
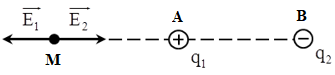
Gọi M là điểm để cường độ điện trường triệt tiêu, khi đó:
\(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}BM - AM = AB\\\dfrac{{A{M^2}}}{{B{M^2}}} = \dfrac{{\left| {{q_1}} \right|}}{{{q_2}}} = \dfrac{9}{{16}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AM - BM = 12cm\\\dfrac{{AM}}{{BM}} = \dfrac{3}{4}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AM = 36cm\\BM = 48cm\end{array} \right.\)
Hướng dẫn giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
- Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\)
- Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\)
