Câu hỏi:
1 năm trước
Cho góc nhọn xBy. Kẻ tia phân giác Bm của góc xBy. Trên tia Bm lấy điểm M bất kì. Kẻ MH vuông góc với Bx, MK vuông góc với By (H \( \in \) Bx, K \( \in \) By). Khẳng định sai là:
Trả lời bởi giáo viên
Đáp án đúng: d
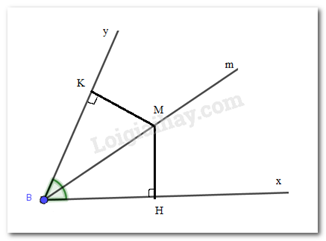
Vì Bm là tia phân giác của góc xBy nên \(\widehat {HBM} = \widehat {KBM}\)
Xét tam giác vuông HBM và KBM, có:
BM chung
\(\widehat {HBM} = \widehat {KBM}\)
\( \Rightarrow \Delta HBM = \Delta KBM\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \)HB = KB; MH = MK ( 2 cạnh tương ứng) nên khẳng định A,B đúng
\(\widehat {BMH} = \widehat {BMK}\)( 2 góc tương ứng), mà tia MB nằm giữa MH và MK nên MA là tia phân giác của góc HMK nên khẳng định C đúng
Hướng dẫn giải:
Sử dụng các trường hợp bằng nhau của tam giác vuông, suy ra các cặp cạnh, cặp góc tương ứng bằng nhau.

