Câu hỏi:
3 năm trước
Cho đường tròn $(O)$ và điểm $I$ nằm ngoài $(O).$Từ điểm $I$ kẻ hai dây cung $AB$ và $CD$ ( $A$ nằm giữa $I$ và $B,C$ nằm giữa $I$ và $D$).
Cặp góc nào sau đây bằng nhau?
Trả lời bởi giáo viên
Đáp án đúng: a
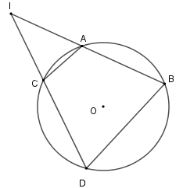
Xét \(\left( O \right)\) có \(\widehat {ACD}\) là góc nội tiếp chắn cung \(AD\) (chứa điểm \(B\) ); \(\widehat {ABD}\) là góc nội tiếp chắn cung $AD$ (chứa điểm \(C\) ) nên \(\widehat {ACD} + \widehat {ABD} = \dfrac{1}{2}.360^\circ = 180^\circ \)
Lại có \(\widehat {ACD} + \widehat {ACI} = 180^\circ \) nên \(\widehat {ACI} = \widehat {IBD}\) .
Tương tự ta có \(\widehat {IAC} = \widehat {IDB}\) .

