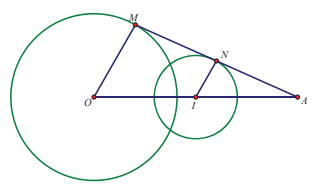
Cho đường tròn \(\left( {O;R} \right)\) và một điểm $A$ cố định. Một điểm $M$ thay đổi trên \(\left( {O;R} \right)\), gọi $N$ là trung điểm của đoạn thẳng $AM$ . Khi $M$ thay đổi trên \(\left( {O;R} \right)\), tập hợp các điểm $N$ là:

Phép biến hình biến điểm $O$ thành điểm $O$ và điểm $M$ khác $O$ thành điểm $M'$  sao cho \(\left( {OM;OM'} \right) = \varphi \) được gọi là phép quay tâm $O$ với góc quay \(\varphi \).

Nếu ${Q_{\left( {O;{{90}^0}} \right)}}:\,\,\,M\,\, \mapsto \,\,M'\,\,\left( {M \ne O} \right)$ thì \(OM' \bot OM\) 

Phép quay không phải là phép dời hình.

Nếu ${Q_{\left( {O;{{90}^0}} \right)}}:\,\,\,M\,\, \mapsto \,\,M'\,\,\left( {M \ne O} \right)$ thì \(OM' > OM\)

Điểm $M\left( {2; - 3} \right)$ là ảnh đối xứng của điểm $N$ qua phép đối xứng trục $Oy$.

Điểm $M\left( { - 2; - 3} \right)$ là ảnh đối xứng của điểm $N$ qua phép đối xứng trục $Ox$.

Điểm $M\left( {2;3} \right)$ là ảnh đối xứng của điểm $N$ qua phép đối xứng trục $Ox$.

Điểm $M\left( { - 2;3} \right)$ là ảnh đối xứng của điểm $N$ qua phép đối xứng trục $Oy$.

Phép dời hình là phép đồng dạng tỉ số $k = 1$ 

Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó

Phép vị tự tỉ số $k > 0$ là phép đồng dạng tỉ số \(k\)

Phép đồng dạng bảo toàn độ lớn góc

\(\left( { - 3;4} \right)\) 

\(\left( { - 4; - 8} \right)\) 

\(\left( {4; - 8} \right)\) 

\(\left( {4;8} \right)\)  

\(\left\{ \begin{array}{l}x' = a + x\\y' = b + y\end{array} \right.\) 

\(\left\{ \begin{array}{l}x' = 2a - x\\y' = 2b - y\end{array} \right.\)

\(\left\{ \begin{array}{l}x' = a - x\\y' = b - y\end{array} \right.\)

\(\left\{ \begin{array}{l}x = 2x' - a\\y = 2y' - b\end{array} \right.\)

Không có phép nào

Có một phép duy nhất

Chỉ có hai phép

Có vô số phép

điểm $M'$ sao cho $MM' = 1$

điểm $M'$ sao cho $MM' = 2$ 

điểm $M'$  sao cho $MM' < 1$ 

chính nó