Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Điểm \(M\) nằm trên \(AB\). Qua \(AB\) kẻ dây \(CD\) tạo với \(AB\) một góc \({45^0}\). Gọi \(D'\) là điểm đối xứng của \(D\) qua \(AB\). Tính \(M{C^2} + MD{'^2}\) theo \(R\)?
Trả lời bởi giáo viên
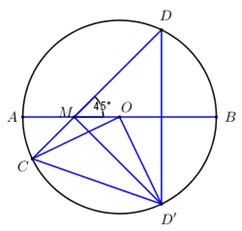
\(D' = \) Đ\(_{AB}\left( D \right) \Rightarrow AB\) là trung trực của \(DD' \Rightarrow MD = MD'\) và \(\angle DMB = \angle D'MB = {45^0}\).
\( \Rightarrow \angle DMD' = {90^0} \Rightarrow \Delta MDD'\) vuông cân tại \(M\).
\( \Rightarrow \angle MDD' = {45^0}\).
Mà \(\angle MDD' = \dfrac{1}{2}\angle COD'\) (góc nội tiếp và góc ở tâm cùng chắn cung \(CD'\))
\( \Rightarrow \angle COD' = {90^0} \Rightarrow \Delta OCD'\) vuông cân tại \(O\).
Do $O\in AB$ là trung trực của \(DD'\Rightarrow OD=OD'=R\Rightarrow D'\in \left( O;R \right)\).
Áp dụng định lí Pytago trong tam giác vuông \(OCD'\) ta có : \(CD{{'}^{2}}=O{{C}^{2}}+OD{{'}^{2}}={{R}^{2}}+{{R}^{2}}=2{{R}^{2}}\).
Ta có \(\angle DMD' = {90^0}\) (cmt) \( \Rightarrow \angle CMD' = {90^0} \Rightarrow \Delta CMD'\) vuông tại \(M\).
Áp dụng định lí Pytago trong tam giác vuông \(CMD'\) ta có : \(M{C^2} + MD{'^2} = CD{'^2} = 2{R^2}\).
Hướng dẫn giải:
Áp dụng định lí Pytago và các tính chất của đường trung trực.

