Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
Trả lời bởi giáo viên
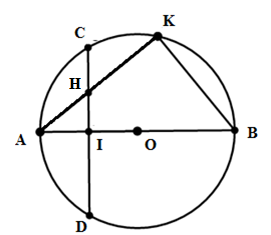
Ta có: \(\widehat {AKB}\) là góc nội tiếp chắn nửa đường tròn (O) \( \Rightarrow \widehat {AKB} = {90^0} \,\left( {t/c} \right).\)
Xét tứ giác $HKBI$ ta có
\(\left\{ \begin{array}{l}\;\widehat {HKB} = {90^0}\\\widehat {HIB} = {90^0}\left( {do\;\;CD \bot AB = \left\{ I \right\}} \right)\end{array} \right. \Rightarrow \widehat {HKB} + \widehat {HIB} = {180^0}\) .
\( \Rightarrow \) Tứ giác $BKHI$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \)phương án A đúng, phương án B sai.
Lại có \(\widehat {KBA} < {90^0}\) do \(\Delta AKB\) vuông tại \(K \Rightarrow KBIH\) không là hình chữ nhật.
\( \Rightarrow \) phương án C sai.
Hướng dẫn giải:
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
Câu hỏi khác
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |