Câu hỏi:
2 năm trước
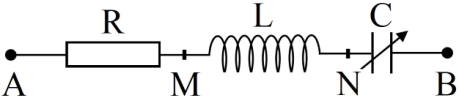
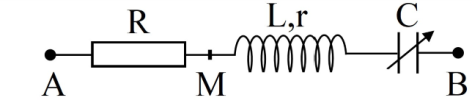Cho đoạn mạch xoay chiều $AB$ nối tiếp gồm: $AM$ chứa biến trở $R$, đoạn mạch $MN$ chứa $r$, đoạn $NP$ chứa cuộn cảm thuần, đoạn $PB$ chứa tụ điện có điện dung biến thiên. Ban đầu thay đổi tụ điện sao cho ${U_{AP}}$ không phụ thuộc vào biến trở $R$. Giữ nguyên giá trị điện dung đó và thay đổi biến trở. Khi${u_{AP}}$ lệch pha cực đại so với ${u_{AB}}$ thì ${U_{PB}} = {U_1}$ . Khi $\left( {{U_{AN}}.{U_{NP}}} \right)$ cực đại thì ${U_{AM}} = {U_2}$. Biết rằng ${U_1} = 2.(\sqrt 6 {\text{}} - \sqrt 3 ){U_2}$ . Độ lệch pha cực đại giữa ${u_{AP}}$ và ${u_{AB}}$ gần nhất với giá trị nào?
Trả lời bởi giáo viên
Đáp án đúng: d
Khi thay đổi \(C\) để \({U_{AP}}\) không phụ thuộc biến trở \(R\) Ta có:
+ Khi R thay đổi ta luôn có \(\Delta APB\) luôn là tam giác cân tại \(A\)
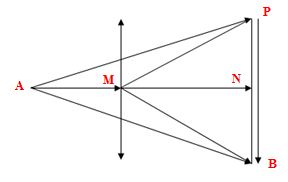
+ Ta thấy khi $R$ thay đổi, nếu ta di chuyển điểm $A \to M$ thì góc $2\varphi $ chính là độ lệch pha của ${U_{AP}}$ và ${U_{AB}}$ và nó càng lớn. Vậy độ lệch pha cực đại của ${U_{AP}}$ và ${U_{AB}}$ khi điểm $A$ trùng với điểm $M$ hay lúc đó $R = 0$.
Khi đó: ${U_1} = {U_{PB}} = \dfrac{U}{{{Z_1}}}.{Z_C} = \dfrac{U}{{\sqrt {{r^2} + Z_L^2} }}.2{Z_L}$
+ Khi $R = {R_0}$ : ${U_{AN}}.{U_{NP}} \le \dfrac{{U_{AN}^2 + U_{NP}^2}}{2} = \dfrac{{{U^2}}}{2}$
Vậy ${U_{AN}}.{U_{NP}}$ lớn nhất khi hay khi đó tam giác $APB$ là tam giác vuông cân.
Lúc này: ${U_2} = {U_{AM}} = \dfrac{U}{{\sqrt 2 }} - {U_r}$
Từ hình vẽ ta suy ra; $\left\{ \begin{gathered} {Z_L} = {\text{ }}R{\text{ }} + {\text{ }}r \hfill \\ {Z_2} = \sqrt 2 .(R + r) \hfill \\\end{gathered} \right.$
Nên : ${U_2} = \dfrac{U}{{\sqrt 2 }} - I.r = \dfrac{U}{{\sqrt 2 }} - \dfrac{U}{{{Z_2}}}.r = \dfrac{U}{{\sqrt 2 }} - \dfrac{U}{{\sqrt 2 .(R + r)}}.r \Rightarrow {U_2} = \dfrac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}$
Lại có, từ đề bài: ${U_1} = 2.(\sqrt 6 {\text{}} + \sqrt 3 ).{U_2}$
Nên ta có:
$\begin{array}{l}\dfrac{U}{{\sqrt {{r^2} + Z_L^2} }}.2.{Z_L} = 2.(\sqrt 6 + \sqrt 3 ).\dfrac{{U.({Z_L} - r)}}{{\sqrt 2 .{Z_L}}}\\ \Rightarrow \dfrac{{{Z_L}}}{{\sqrt {{r^2} + Z_L^2} }} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}\dfrac{{{Z_L} - r}}{{{Z_L}}}\\Z_L^2 = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}.({Z_L} - r).\sqrt {{r^2} + Z_L^2} \Rightarrow {\left( {\dfrac{{{Z_L}}}{r}} \right)^2} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}.\left( {\dfrac{{{Z_L}}}{r} - 1} \right).\sqrt {1 + {{\left( {\dfrac{{{Z_L}}}{r}} \right)}^2}} \end{array}$
Đặt $x = tan\varphi {\text{}} = \dfrac{{{Z_L}}}{r}$ ta có phương trình:
\(\begin{array}{l}{x^2} = \dfrac{{\sqrt 6 + \sqrt 3 }}{{\sqrt 2 }}\left( {x - 1} \right)\sqrt {1 + {x^2}} \\ \to x \approx 1,377\\ \to \varphi \approx {54^0}\\ \to 2\varphi \approx {108^0} \approx \dfrac{3}{5}\pi \end{array}\)
=> Gần với \(\dfrac{{4\pi }}{7}\) nhất
Hướng dẫn giải:
+ C biến thiên để \({U_{RL}}\) không phụ thuộc vào R: \({Z_C} = 2{Z_L}\)
+ Sử dụng giản đồ véc-tơ
+ Sử dụng định luật Ôm và các biến đổi toán học
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
