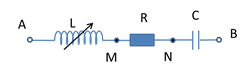
Cho đoạn mạch RLC có L thay đổi được. Đặt vào 2 đầu đoạn mạch hiệu điện thế xoay chiều có tần số f. Khi \(L = {L_1} = \dfrac{2}{\pi }\,\,H\) hoặc \(L = {L_2} = \dfrac{3}{\pi }\,\,H\) thì hiệu điện thế trên cuộn dây thuần cảm này là như nhau. Muốn \({U_{L\max }}\) thì L phải bằng bao nhiêu?

Khi \(L = {L_1}\) và \(L = {L_2}\), điện áp hiệu dụng trên cuộn dây là như nhau, ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{U_{{L_1}}} = \dfrac{{U.{Z_{{L_1}}}}}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_C}} \right)}^2}} }}\\{U_{{L_2}}} = \dfrac{{U.{Z_{{L_2}}}}}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_C}} \right)}^2}} }}\end{array} \right.\\{U_{{L_1}}} = {U_{{L_2}}} \Rightarrow \dfrac{{U.{Z_{{L_1}}}}}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_{{L_2}}}}}{{\sqrt {{R^2} + {{\left( {{Z_{{L_2}}} - {Z_C}} \right)}^2}} }}\\ \Rightarrow {Z_{{L_1}}}^2.\left[ {\sqrt {{R^2} + {{\left( {{Z_{{L_2}}} - {Z_C}} \right)}^2}} } \right] = {Z_{{L_2}}}^2.\left[ {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_C}} \right)}^2}} \right]\\ \Rightarrow \left( {{R^2} + {Z_C}^2} \right).\left( {{Z_{{L_1}}}^2 - {Z_{{L_2}}}^2} \right) - 2{Z_C}{Z_{{L_1}}}{Z_{{L_2}}}.\left( {{Z_{{L_1}}} - {Z_{{L_2}}}} \right) = 0\end{array}\)

Do \({Z_{{L_1}}} \ne {Z_{{L_2}}} \Rightarrow {R^2} + {Z_C}^2 = \dfrac{{2{Z_C}{Z_{{L_1}}}{Z_{{L_2}}}}}{{{Z_{{L_1}}} + {Z_{{L_2}}}}}\)

Hiệu điện thế hiệu dụng trên cuộn dây đạt cực đại khi:

\(\begin{array}{l}{Z_L} = \dfrac{{{R^2} + {Z_C}^2}}{{{Z_C}}} = \dfrac{{\dfrac{{2{Z_C}{Z_{{L_1}}}{Z_{{L_2}}}}}{{{Z_{{L_1}}} + {Z_{{L_2}}}}}}}{{{Z_C}}} = \dfrac{{2{Z_{{L_1}}}{Z_{{L_2}}}}}{{{Z_{{L_1}}} + {Z_{{L_2}}}}}\\ \Rightarrow \dfrac{1}{{{Z_L}}} = \dfrac{1}{2}.\dfrac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{{{Z_{{L_1}}}{Z_{{L_2}}}}} = \dfrac{1}{2}.\left( {\dfrac{1}{{{Z_{{L_1}}}}} + \dfrac{1}{{{Z_{{L_2}}}}}} \right)\\ \Rightarrow \dfrac{1}{{\omega L}} = \dfrac{1}{2}.\left( {\dfrac{1}{{\omega {L_1}}} + \dfrac{1}{{\omega {L_2}}}} \right) \Rightarrow \dfrac{1}{L} = \dfrac{1}{2}.\left( {\dfrac{1}{{{L_1}}} + \dfrac{1}{{{L_2}}}} \right)\\ \Rightarrow \dfrac{1}{L} = \dfrac{1}{2}.\left( {\dfrac{\pi }{2} + \dfrac{\pi }{3}} \right) = \dfrac{{5\pi }}{{12}} \Rightarrow L = \dfrac{{12}}{{5\pi }} = \dfrac{{2,4}}{\pi }\,\,\left( H \right)\end{array}\)