Câu hỏi:
2 năm trước
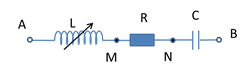
Cho đoạn mạch không phân nhánh RLC có \(R = 30\sqrt 3 \,\,\Omega ;C = \dfrac{{{{5.10}^{ - 4}}}}{{3\pi }}\,\,F\), cuộn dây thuần cảm có độ tự cảm L thay đổi được. Điện áp hiệu dụng giữa hai đầu đoạn mạch là \(u = 100\sqrt 6 \cos \left( {100\pi t + \dfrac{\pi }{3}} \right)\,\,\left( V \right)\). Điều chỉnh L để điện áp hiệu dụng giữa hai đầu đoạn mạch RL cực đại, giá trị đó bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Dung kháng của tụ điện là: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{5.10}^{ - 4}}}}{{3\pi }}}} = 60\,\,\left( \Omega \right)\)
Điện áp hiệu dụng giữa hai đầu RL là:
\({U_{RL}} = \dfrac{{U.\sqrt {{R^2} + {Z_L}^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{{Z_C}^2 - 2{Z_L}{Z_C}}}{{{R^2} + {Z_L}^2}}} }}\)
Để \({U_{RL\max }} \Leftrightarrow {\left( {\dfrac{{{Z_C}^2 - 2{Z_L}{Z_C}}}{{{R^2} + {Z_L}^2}}} \right)_{\min }}\)
Đặt \({Z_L} = x;{f_{\left( x \right)}} = \dfrac{{{Z_C}^2 - 2{Z_C}.x}}{{{R^2} + {x^2}}} \Rightarrow f{'_{\left( x \right)}} = \dfrac{{{x^2} - {Z_C}.x - {R^2}}}{{{{\left( {{R^2} + {x^2}} \right)}^2}}}\)
Ta có: \(f{'_{\left( x \right)}} = 0 \Rightarrow {x^2} - {Z_C}.x - {R^2} = 0 \Rightarrow x = {Z_L} = \dfrac{{{Z_C} \pm \sqrt {{Z_C}^2 - 4{R^2}} }}{2}\)
\(\begin{array}{l} \Rightarrow {Z_L} = \dfrac{{60 + \sqrt {{{60}^2} + 4.{{\left( {30\sqrt 3 } \right)}^2}} }}{2} = 90\,\,\left( \Omega \right)\\ \Rightarrow {U_{RL}} = \dfrac{{100\sqrt 3 .\sqrt {{{\left( {30\sqrt 3 } \right)}^2} + {{90}^2}} }}{{\sqrt {{{\left( {30\sqrt 3 } \right)}^2} + {{\left( {90 - 60} \right)}^2}} }} = 300\,\,\left( V \right)\end{array}\)
Hướng dẫn giải:
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Điện áp hiệu dụng giữa hai đầu RL: \({U_{RL}} = \dfrac{{U.\sqrt {{R^2} + {Z_L}^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Hàm số \({f_{\left( x \right)\min }} \Leftrightarrow f{'_{\left( x \right)}} = 0\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
