Câu hỏi:
2 năm trước
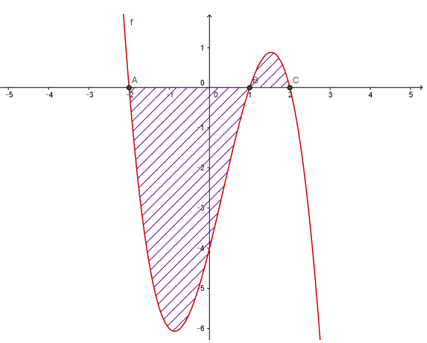
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi
Trả lời bởi giáo viên
Đáp án đúng: b
Nhận thấy phần đồ thị chia làm 2 phần, chú ý đến cận của từng phần.
Phần 1 có cận từ −2 đến 1 nhưng trong (−1;2), đồ thị hàm số nằm phía dưới trục hoành.
Phần 2 có cận từ 1 đến 2 và đồ thị hàm số nằm phía trên trục hoành.
Vậy S=∫1−2(−f(x))dx+∫21f(x)dx=∫−21f(x)dx+∫21f(x)dx
Hướng dẫn giải:
- Bước 1: Giải phương trình f(x)=g(x) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức |f(x)−g(x)|
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân S=b∫a|f(x)−g(x)|dx
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án A vì không nhớ kĩ công thức tính diện tích.

