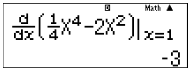Cho điểm M thuộc đồ thị \(\left( C \right):y = \dfrac{1}{4}{x^4} - 2{x^2}\) có hoành độ \({x_0} > 0\) và \(y''\left( {{x_0}} \right) = - 1\). Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm M có dạng \(y = ax + b\). Tính \(a - b\)
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Ta có: \(y' = {x^3} - 4x,y'' = 3{x^2} - 4\)
Khi đó: \(y''\left( {{x_0}} \right) = - 1 \Leftrightarrow 3x_0^2 - 4 = - 1 \Leftrightarrow {x_0} = \pm 1\)
Do \({x_0} > 0 \Rightarrow {x_0} = 1\)
Thay vào y ta được: \({y_0} = y\left( 1 \right) = - \dfrac{7}{4}\)
Hệ số góc là \(k = y'\left( 1 \right) = {1^3} - 4.1 = - 3\)
Khi đó phương trình tiếp tuyến cần tìm là
\(y=-3(x-1)-\dfrac{7}{4}=-3x+\dfrac{5}{4}\)
Hướng dẫn giải:
Bước 1: Tính y’ và y’’
Bước 2: Giải phương trình \(y''\left( {{x_0}} \right) = - 1\) tìm \({x_0}\)
Bước 3: Tìm \({y_0} = y\left( {{x_0}} \right)\) và hệ số góc \(k = y'\left( {{x_0}} \right)\)
Bước 4: Tìm a, b và tính a-b
Giải thích thêm:
Tính đạo hàm tại \({x_0} = 1\) bằng máy tính cầm tay:
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
