Câu hỏi:
2 năm trước
Cho \(\Delta ABC\), trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia Ax sao cho \(\widehat {CAx} = \widehat {ACB}\). Trên nửa mặt phẳng bờ AB không chứa điểm C, vẽ tia Ay sao cho \(\widehat {BAy} = \widehat {ABC}\). Qua C kẻ đường thẳng d vuông góc với BC. Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: c
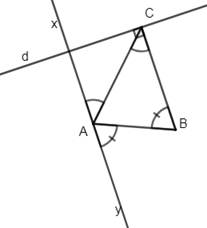
+) Ta có: \(\widehat {CAx} = \widehat {ACB}\left( {gt} \right)\) mà hai góc đó là hai góc so le trong nên
suy ra \(Ax//\,BC\) (1) (nên A đúng)
\(\widehat {BAy} = \widehat {ABC}\left( {gt} \right)\) mà hai góc đó là hai góc so le trong nên suy ra \(Ay//\,BC\) (2)
Từ (1) và (2) suy ra Ax và Ay cùng song song với BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
\( \Rightarrow \) Ax và Ay là hai tia đối nhau nên D đúng.
+) Vì Ax và Ay là hai tia đối nhau (cmt) mà \(Ax//\,BC\) và \(Ay//\,BC\)
nên suy ra \(xy//\,BC\) nên C sai.
Mà \(BC \bot d\) nên suy ra \(d \bot xy\) nên B đúng.
Hướng dẫn giải:
Áp dụng dấu hiệu nhận biết hai đường thẳng song song, quan hệ giữa tính vuông góc và tính song song.
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
