Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(\widehat A = {90^0}\), các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I. Gọi $D,E$ là chân các đường vuông góc hạ từ $I$ đến các cạnh $AB$ và $AC.$ Khi đó ta có:
Trả lời bởi giáo viên
Đáp án đúng: d
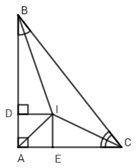
Xét \(\Delta ABC\) có các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I nên I là giao điểm của ba đường phân giác trong \(\Delta ABC\), suy ra AI là đường phân giác của \(\widehat A\) và I cách đều ba cạnh của \(\Delta ABC\) (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A, B và C.
Vì I là giao điểm của ba đường phân giác trong \(\Delta ABC\) nên \( \Rightarrow DI = IE\) (tính chất 3 đường phân giác của tam giác).
Hướng dẫn giải:
Áp dụng tính chất 3 đường phân giác của tam giác.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
