Cho \(\Delta ABC\) có: \(\widehat A = {140^0}.\) Các đường trung trực của các cạnh \(AB\) và \(AC\) cắt nhau tại \(I.\) Tính số đo góc \(BIC.\)
Trả lời bởi giáo viên
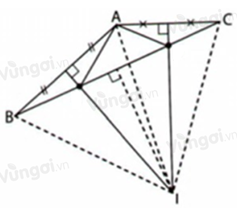
Vì \(\Delta ABC\) có các đường trung trực của các cạnh \(AB\) và \(AC\) cắt nhau tại \(I\) nên \(IA = IB = IC\) (tính chất ba đường trung trực của tam giác).
Xét \(\Delta IAB\) có: \(IA = IB\) (cmt) \( \Rightarrow \Delta IAB\) cân tại \(I\) (dấu hiệu nhận biết tam giác cân) \( \Rightarrow \widehat {IAB} = \widehat {IBA}\) (tính chất tam giác cân).
Xét \(\Delta IAC\) có: \(IA = IC\) (cmt) \( \Rightarrow \Delta IAC\) cân tại \(I\) (dấu hiệu nhận biết tam giác cân) \( \Rightarrow \widehat {IAC} = \widehat {ICA}\) (tính chất tam giác cân).
Trong \(\Delta IAB\) có: \(\widehat {BIA} + \widehat {IAB} + \widehat {IBA} = {180^0}\) (định lí tổng ba góc của một tam giác)
Mà \(\widehat {IAB} = \widehat {IBA}(cmt)\) suy ra \(\widehat {BIA} = {180^0} - (\widehat {IAB} + \widehat {IBA}) = {180^0} - 2.\widehat {IAB}\)
Trong \(\Delta IAC\) có: \(\widehat {AIC} + \widehat {IAC} + \widehat {ICA} = {180^0}\) (định lí tổng ba góc của một tam giác)
Mà \(\widehat {IAC} = \widehat {ICA}(cmt)\) suy ra \(\widehat {AIC} = {180^0} - (\widehat {IAC} + \widehat {ICA}) = {180^0} - 2.\widehat {IAC}\)
Khi đó \(\widehat {BIC} = \widehat {BIA} + \widehat {AIC} = {180^0} - 2.\widehat {IAB} + {180^0} - 2.\widehat {IAC}\)
\( = {360^0} - 2.(\widehat {IAB} + \widehat {IAC}) = {360^0} - 2.\widehat {BAC} = {360^0} - {2.140^0} = {80^0}\).
Hướng dẫn giải:
+ Sử dụng tính chất ba đường trung trực của tam giác: “Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó”, chứng minh \(IA = IB = IC\)
+ Sử dụng tính chất tam giác cân, định lí tổng ba góc của một tam giác tính \(\widehat {BIA};\widehat {AIC}\), khi đó tính được \(\widehat {BIC}\).

