Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Gọi $D$ là một điểm nằm giữa $A$ và $M.$ Khi đó \(\Delta BDC\) là tam giác gì?
Trả lời bởi giáo viên
Đáp án đúng: a
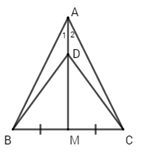
Vì \(\Delta ABC\) cân tại A (gt) và AM là trung tuyến nên AM cũng là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác)
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(AB = AC\left( {gt} \right)\)
\(\widehat {{A_1}} = \widehat {{A_2}}\left( {cmt} \right)\)
AD chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right) \Rightarrow BD = DC\) (2 cạnh tương ứng)
\( \Rightarrow \Delta BDC\) cân tại D (dấu hiệu nhận biết tam giác cân)
Hướng dẫn giải:
Áp dụng tính chất: Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 1 Toán 7 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 7: quan hệ giữa các yếu tố trong tam giác. các đường đồng quy trong tam giác - đề số 2 Toán 7 có lời giải chi tiết
