Cho \(\Delta ABC\), các tia phân giác của góc $B$  và $A$ cắt nhau tại điểm $O.$  Qua $O$  kẻ đường thẳng song song với $BC$  cắt $AB$  tại $M,$ cắt $AC$  ở $N.$  Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$

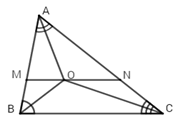
Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\)(gt)

Suy ra, CO là phân giác của \(\widehat {ACB}\)(tính chất 3 đường phân giác của tam giác)

\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)

BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)

Vì MN // BC (gt) \(\left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong)

Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {NCO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow NO = NC = 3cm\) (tính chất tam giác cân)

Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {MBO} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow MB = MO = 2cm\) (tính chất tam giác cân)

\( \Rightarrow MN = MO + ON = 2 + 3 = 5cm.\)