Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh AD = 3cm; AB = 4cm. Các điện tích q1, q2, q3 đặt lần lượt tại A, B, C. Gọi \(\overrightarrow {{E_2}} \) là véctơ cường độ điện trường do điện tích q2 gây ra tại D. \(\overrightarrow {{E_{13}}} \)là cường độ điện trường tổng hợp do các điện tích q1 và q3 gây ra tại D. Xác định giá trị của q1 và q3 biết q2 = -12,5.10-8C và \(\overrightarrow {{E_{13}}} = \overrightarrow {{E_2}} \)
Trả lời bởi giáo viên
Gọi \(\overrightarrow {{E_A}} ,\overrightarrow {{E_B}} ,\overrightarrow {{E_C}} \) lần lượt là cường độ điện trường do điện tích q1, q2 và q3 gây ra tại D.
Ta có: q2 < 0 => \(\overrightarrow {{E_2}} \) hướng về B
Theo đề bài, ta có: \(\overrightarrow {{E_{13}}} = \overrightarrow {{E_2}} \)=> \(\overrightarrow {{E_{13}}} \)phải cùng chiều và có độ lớn bằng \(\overrightarrow {{E_2}} \). Do đó, \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \)và \(\overrightarrow {{E_{13}}} \)có phương, chiều như hình vẽ:
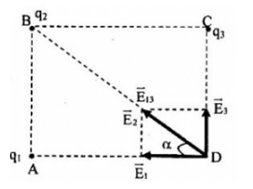
Từ hình vẽ, ta có:
Với \(\left\{ \begin{array}{l}{\rm{cos}}\alpha {\rm{ = }}\frac{{AD}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{3}{{\sqrt {{3^2} + {4^2}} }} = \frac{3}{5}\\\sin \alpha = \frac{{AB}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{4}{{\sqrt {{3^2} + {4^2}} }} = \frac{4}{5}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{B{D^2}}} = {9.10^9}\frac{{\left| { - 12,{{5.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = {45.10^4}V/m\end{array} \right.\)
Ta suy ra:
\(\left\{ \begin{array}{l}{E_1} = {E_2}{\rm{cos}}\alpha = {45.10^4}.\frac{3}{5} = {27.10^4}V/m\\{E_3} = {E_2}\sin \alpha = {45.10^4}.\frac{4}{5} = {36.10^4}V/m\end{array} \right.\)
Mặt khác:
\(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{A{D^2}}} = {27.10^4}V/m\\{E_3} = k\frac{{\left| {{q_1}} \right|}}{{C{D^2}}} = {36.10^4}V/m\end{array} \right. \to \left\{ \begin{array}{l}\left| {{q_1}} \right| = 2,{7.10^{ - 8}}C\\\left| {{q_2}} \right| = 6,{4.10^{ - 8}}C\end{array} \right.\)
Ta thấy, \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \)hướng lại gần các điện tích nên q1 và q3 sẽ là các điện tích âm
\( \to \left\{ \begin{array}{l}{q_1} = - 2,{7.10^{ - 8}}C\\{q_2} = - 6,{4.10^{ - 8}}C\end{array} \right.\)
Hướng dẫn giải:
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)


