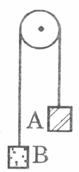
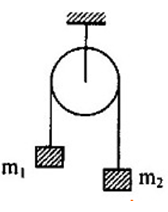
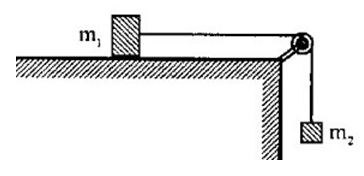
Ba vật có cùng khối lượng m = 200g được nối với nhau bằng dây nối không dãn như hình vẽ. Hệ số ma sát trượt gjữa vật và mặt bàn là \(\mu  = 0,2\). Lấy \(g = 10\left( {m/{s^2}} \right)\). Tính gia tốc khi hệ chuyển động.

Một xe tải kéo một ô tô bằng dây cáp. Từ trạng thái đứng yên sau 100s ô tô đạt vận tốc \(v = 36km/h\). Khối lượng ô tô là \(m = 1000kg\). Lực ma sát bằng 0,01 trọng lực ô tô. Tính lực kéo của xe tải trong thời gian trên. Lấy \(g = 10m/{s^2}\)

Hai vật A và B có thể trượt trên mặt bàn nằm ngang và được nối với nhau bằng dây không dẫn, khối lượng không đáng kể. Khối lượng 2 vật là \({m_A} = 2kg,{m_B} = 1kg\), ta tác dụng vào vật A một lực F = 9N theo phương song song với mặt bàn. Hệ số ma sát giữa hai vật với mặt bàn là \(\mu  = 0,2\). Lấy \(g = 10\left( {m/{s^2}} \right)\). Hãy tính gia tốc chuyển động.

Hai vật A và B có khối lượng lần lượt là \({m_A} = 600g,{m_B} = 400g\) được nối với nhau bằng sợi dây nhẹ không dãn và vắt qua ròng rọc cố định như hình vẽ. Bỏ qua khối lượng của ròng rọc và lực ma sát giữa dây với ròng rọc. Lấy g = 10m/s2. Tính gia tốc chuyển động của mối vật.

Cho hệ vật như hình vẽ:

Biết \({m_1} = 2{m_2}\). Lực căng của dây treo ròng rọc là \(52,3N\). Khối lượng của \({m_2}\) có giá trị là:

Cho cơ hệ như hình vẽ:

Cho \({m_1} = 1,6kg;{m_2} = 400g,g = 10m/{s^2}\), bỏ qua ma sát, khối lượng dây và ròng rọc. Lực nén lên trục của ròng rọc là:

Một xe trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng với góc \(\alpha  = {30^ \circ }\). Hệ số ma sát trượt là \(\mu  = 0,3464\). Chiều dài mặt phẳng nghiêng là \(l = 1m\). Lấy \(g = 10m/{s^2}\) và \(\sqrt 3  = 1,732\). Gia tốc của chuyển động là: