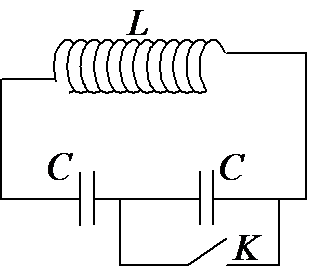
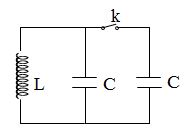
Ăng-ten sử dụng một mạch dao động \(LC\) lý tưởng để thu sóng điện từ, trong đó cuộn dây có \(L\) không đổi, tụ điện có điện dung \(C\) thay đổi được. mỗi sóng điện từ đều tạo ra trong mạch dao động một suất điện động cảm ứng. Xem rằng các sóng điện từ có biên độ cảm ứng từ đều bằng nhau. Khi điện dung của tụ điện \({C_1} = 1\mu F\) thì suất điện động cảm ứng hiệu dụng trong mạch do sóng điện từ tạo ra là \({E_1} = 4,5\mu V\). Khi điện dung của tụ điện \({C_2} = 9\mu F\) thì suất điện động cảm ứng hiệu dụng do sóng điện từ tạo ra là:

Một mạch dao động \(LC\) lí tưởng được mắc với nguồn điện có suất điện động \(6\;V\), điện trở trong không đáng kể (hình vẽ bên). Điện dung của tụ điện là \(0,5\mu F;\) độ tự cảm của cuộn dây là \(2mH\). Lấy \({\pi ^2} = 10.\) Ban đầu khóa \({\rm{k}}\) ngắt tụ điện chưa tích điện, tại thời điểm \(t = 0\) người ta đóng khóa \({\rm{k}}\) thì trong mạch có dao động điện từ tự do. Kể từ \(t = 0\), thời điểm mà cường độ dòng điện trong mạch có độ lớn \(15\sqrt 3 \pi ({\rm{mA}})\) lần thứ 3 thì điện tích của bản tụ điện nối với khóa \({\rm{k}}\) có giá trị là

Hai tụ điện \({C_1} = {\rm{ }}{C_2}\) mắc song song. Nối hai đầu bộ tụ với ắc qui có suất điện động \(E{\rm{ }} = {\rm{ }}6V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm \(L\) để tạo thành mạch dao động. Sau khi dao động trong mạch đã ổn định, tại thời điểm dòng điện qua cuộn dây có độ lớn bằng một nữa giá trị dòng điện cực đại, người ta ngắt khóa K để cho mạch nhánh chứa tụ \({C_2}\) hở. Kể từ đó, hiệu điện thế cực đại trên tụ còn lại \({C_1}\) là:

Hai tụ điện \({C_1} = {\rm{ }}3{C_0}\) và \({C_2} = {\rm{ }}6{C_0}\) mắc nối tiếp. Nối hai đầu bộ tụ với pin có suất điện động  \(E{\rm{ }} = {\rm{ }}3V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm \(L\) tạo thành mạch dao động điện từ tự do. Tại thời điểm dòng điện qua cuộn dây có độ lớn bằng một nửa giá trị dòng điện đạt cực đại, thì người ta nối tắt hai cực của tụ \({C_1}\). Điện áp cực đại trên tụ \({C_2}\) của mạch dao động sau đó:

Hai tụ \({C_1} = 3{C_0}\) và \({C_2} = {\rm{ }}6{C_0}\) mắc nối tiếp. Nối \(2\) đầu bộ tụ với pin có suất điện động \(E = {\rm{ }}3V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm L tạo thành mạch dao động điện từ tự do. Khi dòng điện trong mạch dao động đạt cực đại thì người ta nối tắt 2 cực của tụ \({C_1}\). Hiệu điện thế cực đại trên tụ \({C_2}\) của mạch dao động sau đó là:

Mạch dao động điện từ lí tưởng gồm cuộn dây thuần cảm và hai tụ điện giống hệt nhau ghép nối tiếp. Hai bản của một tụ được nối với nhau bằng khóa K. Ban đầu khóa K mở. Cung cấp năng lượng cho mạch dao động thì điện áp  cực đại giữa hai đầu cuộn cảm là \(8\sqrt 6 V\) . Sau đó vào đúng thời điểm dòng điện qua cuộn dây có cường độ bằng giá trị hiệu dụng thì đóng khóa K. Hiệu điện thế cực đại giũa hai đầu cuộn dây sau khi đóng khóa K:

Một mạch dao động LC lí tưởng gồm cuộn thuần cảm L và hai tụ điện C giống nhau mắc nối tiếp. Mạch đang hoạt động thì ngay tại thời điểm nặng lượng điện trường trong tụ gấp đôi năng lượng từ trường trong cuộn cảm, một tụ bị đánh thủng hoàn toàn. Điện áp cực đại hai đầu cuộn cảm đó sẽ bằng bao nhiêu lần so với lúc đầu?

Mạch dao động điện từ gồm cuộn cảm và một bộ hai tụ điện có cùng điện dung \(C = 2,5\mu F\) mắc song song. Trong mạch có dao động điện từ tự do, hiệu điện thế cực đại giữa hai bản tụ điện là \({U_0} = 12V\). Tại thời điểm hiệu điện thế hai đầu cuộn cảm \({u_L} = 6V\) thì một tụ điện bị bong ra vì đứt dây nối. Tính năng lượng cực đại trong cuộn cảm sau đó: