Câu hỏi tr 113
| Câu hỏi: Hãy cho ví dụ về hệ kín. |
Phương pháp giải:
- Một hệ nhiều vật được gọi là hệ kín khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các lực ấy cân bằng nhau.
- Trong một hệ kín, chỉ có các nội lực tương tác giữa các vật. Các nội lực này theo định luật III Newton trực đối nhau từng đôi một.
Lời giải chi tiết:
Ví dụ:
- Hai xe va chạm nhau trên đệm khí
- Một viên bi đang đứng yên, một viên khác đi tới chạm vào viên bi đứng yên.
Câu hỏi tr 114
Câu hỏi
| Một hệ gồm hai vật có khối lượng lần lượt là m1 và m2 , chuyển động với vận tốc có độ lớn lần lượt là v1 và v2 hướng vào nhau. Bỏ qua mọi ma sát và lực cản của không khí. Viết biểu thức của định luật bảo toàn động lượng cho hệ này. |
Phương pháp giải:
Định luật bảo toàn động lượng: Động lượng toàn phần của hệ kín là một đại lượng được bảo toàn.
\(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Lời giải chi tiết:
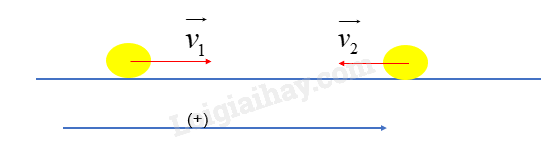
Chọn chiều dương như hình vẽ
Áp dụng định luật bảo toàn động lượng, ta có: \(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} = {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \)
Chiếu lên chiều dương của chuyển động, ta có: \(p = {m_1}.{v_1} - {m_2}.{v_2}\)
Câu hỏi
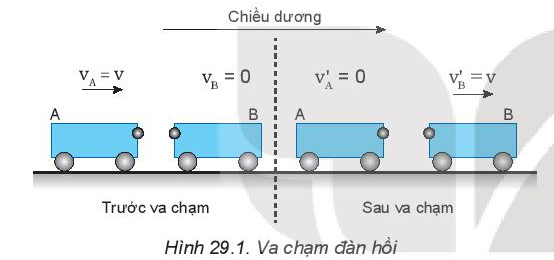
| Câu 1: Hãy tính động lượng và động năng của hệ trước và sau va chạm đàn hồi (Hình 29.1).
|
Phương pháp giải:
- Biểu thức tính động lượng: p = m.v
- Biểu thức tính động năng: \(W = \frac{1}{2}.m.{v^2}\)
Lời giải chi tiết:
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_B' = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.{v^2}\)
| Câu 2: Từ kết quả tính được rút ra nhận xét gì? |
Phương pháp giải:
Áp dụng kết quả của câu 1
Lời giải chi tiết:
Từ kết quả tính được, ta thấy trong va chạm đàn hồi, động lượng được bảo toàn, năng lượng được bảo toàn.
Câu hỏi tr 115
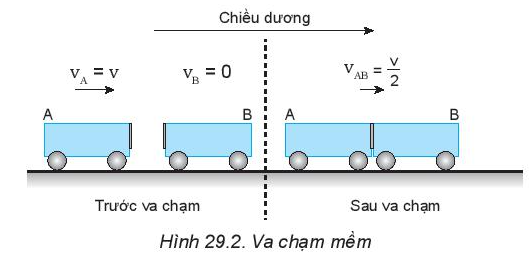
| Câu 1: Hãy tính động lượng và động năng của hệ trong Hình 29.2 trước và sau va chạm.
|
Phương pháp giải:
- Biểu thức tính động lượng: p = m.v
- Biểu thức tính động năng: \(W = \frac{1}{2}.m.{v^2}\)
Lời giải chi tiết:
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_A^' + m.v_B^' = m.(v_A^' + v_B^') = m.\left( {\frac{v}{2} + \frac{v}{2}} \right) = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_A^{'2} + \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.\left( {\frac{{{v^2}}}{4} + \frac{{{v^2}}}{4}} \right) = \frac{1}{4}.m.{v^2}\)
| Câu 2: Từ kết quả tính được rút ra nhận xét gì? |
Phương pháp giải:
Áp dụng kết quả từ câu 1
Lời giải chi tiết:
Từ kết quả câu 1, ta thấy trong va chạm mềm thì động lượng không thay đổi (được bảo toàn), động năng thay đổi (năng lượng không được bảo toàn).
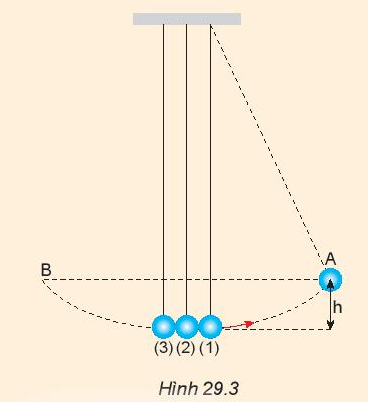
| Câu 3: Trong Hình 29.3, nếu kéo bi (1) lên thêm một độ cao h rồi thả ra. Con lắc sẽ rơi xuống và va chạm với hai con lắc còn lại. Hãy dự đoán xem va chạm là va chạm gì. Con lắc (2), (3) lên tới độ cao nào? Làm thí nghiệm để kiểm tra.
|
Phương pháp giải:
Quan sát hình vẽ, làm thí nghiệm
Lời giải chi tiết:
- Va chạm là va chạm đàn hồi.
- Con lắc (3) lên tới vị trí B, con lắc (2) ở dưới vị trí B.
- Các em tự làm thí nghiệm để kiểm tra.