Câu hỏi tr 120
| Mở đầu: Khi xe mô tô đua vào khúc cua thì có những bộ phận nào của xe chuyển động tròn?
|
Phương pháp giải:
Quan sát hình và vận dụng thực tế
Lời giải chi tiết:
Khi xe mô tô đua vào khúc cua thì bộ phận của xe chuyển động tròn là: bánh xe.
Câu hỏi
| Câu 1: Chứng minh rằng một radian là góc ở tâm chắn cung có độ dài bằng bán kính đường tròn. |
Phương pháp giải:
Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
Lời giải chi tiết:
Ta có \(\theta \) = 1 rad
\( \Rightarrow \theta = \frac{s}{r} = 1 \Rightarrow s = r\)
Vậy góc chắn tâm bằng 1 radian thì độ dài cung bằng bán kính đường tròn.
| Câu 2: Tính quãng đường đi được khi vật chuyển động tròn có độ dịch chuyển góc 1 rad, biết bán kính đường tròn là 2 m. |
Phương pháp giải:
Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (độ dịch chuyển góc) (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
Lời giải chi tiết:
Ta có \(\theta \) = 1 rad
\( \Rightarrow \theta = \frac{s}{r} = 1 \Rightarrow s = r = 2(m)\)
| Câu 3: Xét chuyển động của kim giờ đồng hồ. Tìm độ dịch chuyển góc của nó (theo độ và radian): a) Trong mỗi giờ. b) Trong khoảng thời gian từ 12 h đến 15 h 30 min. |
Phương pháp giải:
- Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (độ dịch chuyển góc) (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
- 1. Π = 1800
Lời giải chi tiết:
a) Ta có 1 vòng tròn tương ứng là 2π rad
=> 1 giờ vật quay được góc của đồng hồ
=> Độ dịch chuyển góc của kim giờ trong 1 giờ đồng hồ là \(\frac{{2\pi }}{{12}} = \frac{\pi }{6}\)
Đổi \(\frac{\pi }{6} = {\left( {\frac{\pi }{6}.\frac{{180}}{\pi }} \right)^0} = {30^0}\)
b)
Từ 12 h đến 15 h 30 min, độ dịch chuyển thời gian là 3 h 30 min = 3,5 giờ
Ta có 1 giờ vật quay được góc của đồng hồ
=> 3,5 h vật quay được \(3,5.\frac{1}{{12}} = \frac{7}{{24}}\) góc đồng hồ
=> Độ dịch chuyển góc của kim giờ trong 3,5 h đồng hồ là \(2\pi .\frac{7}{{24}} = \frac{{7\pi }}{{12}}\)
Đổi \(\frac{{7\pi }}{{12}} = {\left( {\frac{{7\pi }}{{12}}.\frac{{180}}{\pi }} \right)^0} = {105^0}\)
Câu hỏi tr 121
Câu hỏi: Dựa vào việc quan sát chuyển động của kim giây trong đồng hồ có kim trôi để:
| Câu 1: So sánh tốc độ của các điểm khác nhau trên kim |
Phương pháp giải:
Quan sát chuyển động của các kim trên đồng hồ
Lời giải chi tiết:
Ta thấy tốc độ của các điểm khi kim giây chuyển động là như nhau trên đường tròn
| Câu 2: So sánh độ dịch chuyển góc trong cùng khoảng thời gian của các điểm khác nhau trên kim. |
Phương pháp giải:
Quan sát chuyển động của kim giây trên đồng hồ
Lời giải chi tiết:
Độ dịch chuyển góc trong cùng khoảng thời gian của các điểm khác nhau trên kim là như nhau.
Câu hỏi
| Câu 1: Hãy tính tốc độ góc của kim giờ và kim phút của đồng hồ. |
Phương pháp giải:
Mối liên hệ giữa chu kì và tốc độ góc trong chuyển động tròn đều là: \(\omega = \frac{{2\pi }}{T}\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
Lời giải chi tiết:
Chu kì quay của kim giờ là 12 giờ = 1 036 800 s
Chu kì quay của kim phút là 60 phút = 3600 s
Tốc độ góc của kim giờ là: \({\omega _h} = \frac{{2\pi }}{{{T_h}}} = \frac{{2\pi }}{{1036800}} \approx {6.10^{ - 6}}(rad/s)\)
Tốc độ góc của kim phút là: \({\omega _{ph\'u t}} = \frac{{2\pi }}{{{T_{ph\'u t}}}} = \frac{{2\pi }}{{3600}} \approx 1,{75.10^{ - 3}}(rad/s)\)
| Câu 2: Roto trong một tổ máy thủy điện Hòa Bình quay 125 vòng mỗi phút. Hãy tính tốc độ góc của roto này theo đơn vị rad/s. |
Phương pháp giải:
Mối liên hệ giữa tần số và tốc độ góc: \(\omega = 2\pi f\)
Trong đó:
+ \(\omega \): tốc độ góc (rad/s)
+ f: tần số (vòng/s hoặc Hz)
Lời giải chi tiết:
Ta có f = 125 vòng/phút = vòng/s
Tốc độ góc của roto là: \(\omega = 2\pi f = 2\pi .\frac{{25}}{{12}} \approx 13,1(rad/s)\)
Câu hỏi
| Câu 1:Biết chiều dài kim phút và kim giây của một chiếc đồng hồ lần lượt là 4 cm và 5 cm. Hãy tính: a) Tỉ số chu kì quay của hai kim. b) Tỉ số tốc độ của đầu kim phút và đầu kim giây. |
Phương pháp giải:
- Chu kì quay trong chuyển động tròn đều là: \(T = \frac{{2\pi }}{\omega }\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
- Mối liên hệ giữa tốc độ và tốc độ góc trong chuyển động tròn đều là: \(v = \omega .r\)
Lời giải chi tiết:
a) Chu kì là khoảng thời gian để vật quay hết một vòng tròn
+ Chu kì quay của kim phút là 60 phút = 3600 giây
+ Chu kì quay của kim giây là 60 giây
b) Ta có: \(v = \omega .r = \frac{{2\pi }}{T}.r\)
\(\begin{array}{l}{v_{ph\'u t}} = \frac{{2\pi }}{{{T_{ph\'u t}}}}.{r_{ph\'u t}}\\{v_{gi\^a y}} = \frac{{2\pi }}{{{T_{gi\^a y}}}}.{r_{gi\^a y}}\end{array}\)
\( \Rightarrow \frac{{{v_{ph\'u t}}}}{{{v_{gi\^a y}}}} = \frac{{{r_{ph\'u t}}}}{{{r_{gi\^a y}}}}.\frac{{{T_{gi\^a y}}}}{{{T_{ph\'u t}}}} = \frac{4}{5}.\frac{{60}}{{3600}} = \frac{1}{{75}}\)
| Câu 2:Xét một điểm nằm trên đường xích đạo trong chuyển động tự quay của Trái Đất. Biết bán kính Trái Đất tại xích đạo là 6 400 km. Hãy tính: a) Chu kì chuyển động của điểm đó. b) Tốc độ và tốc độ góc của điểm đó. |
Phương pháp giải:
Trái Đất tự quay quanh trục của nó 1 vòng hết 24 giờ
- Chu kì quay trong chuyển động tròn đều là: \(T = \frac{{2\pi }}{\omega }\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
- Mối liên hệ giữa tốc độ và tốc độ góc trong chuyển động tròn đều là: \(v = \omega .r\)
Lời giải chi tiết:
a) Trái Đất tự quay quanh trục của nó 1 vòng hết 24 giờ
=> Chu kì chuyển động của một điểm trong chuyển động tự quay của Trái Đất là 24 giờ.
b) Đổi 24 giờ = 2 073 600 s; 6400 km = 6,4.106 m.
Tốc độ góc của điểm đó là: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{2073600}} \approx {3.10^{ - 6}}(rad/s)\)
Tốc độ của điểm đó là:
\(v = \omega .r = {3.10^{ - 6}}.6,{4.10^6} = 19,2(m/s)\)
Câu hỏi tr 122
Câu hỏi
| Câu 1: Phân biệt tốc độ và độ lớn của vận tốc trong chuyển động tròn đều. |
Phương pháp giải:
Vận dụng lí thuyết trong sách giáo khoa trang 121-122
Lời giải chi tiết:
+ Vận tốc có độ lớn không đổi nhưng hướng luôn thay đổi ( vận tốc là đại lượng vecto)
+ Tốc độ có độ lớn và hướng không đổi (tốc độ là đại lượng vô hướng).
| Câu 2: Nêu mối quan hệ giữa tốc độ v, chu kì T và bán kính r của một vật chuyển động tròn đều |
Phương pháp giải:
- Chu kì quay trong chuyển động tròn đều là: \(T = \frac{{2\pi }}{\omega }\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
Lời giải chi tiết:
- Mối liên hệ giữa tốc độ và tốc độ góc trong chuyển động tròn đều là: \(v = \omega .r\)
=> v tỉ lệ thuận với r.
- Ta có: \(v = \omega .r = \frac{{2\pi }}{T}.r\)
Trong chuyển động tròn đều, v tỉ lệ nghịch với T.
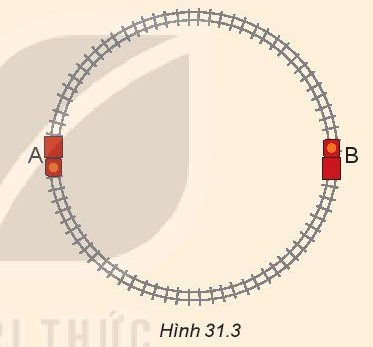
| Câu 3: Một xe đồ chơi chạy với tốc độ không đổi 0,2 m/s trên một đường ray tròn tâm O, đường kính AB theo chiều kim đồng hồ. (Hình 31.3) Xác định sự thay đổi vận tốc khi xe đi từ A đến B
|
Phương pháp giải:
Trong chuyển động tròn đều, vận tốc đều có độ lớn không đổi
Lời giải chi tiết:
Khi xe đi từ A đến B thì vận tốc của xe không đổi nhưng hướng thay đổi, vận tốc của xe là 0,2 m/s.