Câu hỏi:
2 năm trước
Xác định giá trị của tham số $m$ để hàm số $y = {x^3} - 3m{x^2} - m$ nghịch biến trên khoảng $\left( {0;1} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: $y' = 3{{\rm{x}}^2} - 6m{\rm{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2m$
Trường hợp 1: $m < 0$
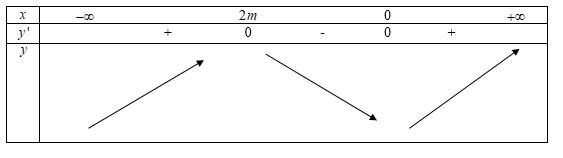
Dễ thấy hàm số trên khoảng $\left( {0;1} \right)$ đồng biến với mọi $m < 0$(loại)
Trường hợp 2: $m = 0$
Với $m=0$ thì $y'=3x^2 \ge 0$ nên hàm số đồng biến trên $R$ .
Do đó hàm số đồng biến trên $\left( {0;1} \right)$ (loại)
Trường hợp 3: $m > 0$
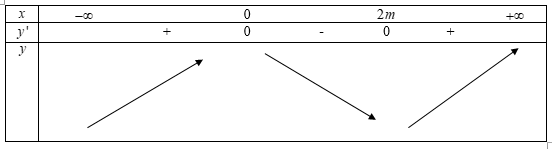
Dễ thấy hàm số trên khoảng $\left( {0;1} \right)$ nghịch biến $ \Leftrightarrow 2m \ge 1 \Leftrightarrow m \ge \dfrac{1}{2}$
Hướng dẫn giải:
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên D:
+ Hàm số $y = f\left( x \right)$ nghịch biến trên $D \Leftrightarrow y' = f'\left( x \right) \le 0$ với mọi $x \in D$
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm $m$.
+ Biện luận theo $m$ để xét dấu đạo hàm.
- Bước 3: Kết luận.
Giải thích thêm:
Một số em sẽ bị nhầm khi cho rằng hàm số nghịch biến trên $\left( {0;1} \right) \Leftrightarrow $$2m < 1 \Leftrightarrow m < \dfrac{1}{2}$ dẫn đến chọn sai đáp án.
Có thể giải bài toán bằng cách khác:
Ở bước cho $y' < 0,\forall x \in \left( {0;1} \right)$ ta có:
$y' = 3{x^2} - 6mx \le 0,\forall x \in \left( {0;1} \right) \Leftrightarrow m \ge \dfrac{x}{2},\forall x \in \left( {0;1} \right)$ (do $x > 0$)
Lại có $0 < x < 1 \Leftrightarrow 0 < \dfrac{x}{2} < \dfrac{1}{2}$ nên $m \ge \dfrac{x}{2},\forall x \in \left( {0;1} \right) \Leftrightarrow m \ge \dfrac{1}{2}$.
Câu hỏi khác
- Bài tập phần cực trị của hàm số thi ĐGNL ĐHQG HN
- Bài tập phần bài toán liên quan đến khảo sát hàm số bậc ba, bậc bốn trùng phương có tham số thi ĐGNL ĐHQG HN
- Bài tập phần bài toán cực trị có tham số đối với một số hàm số cơ bản thi ĐGNL ĐHQG HN
- Bài tập phần giá trị lớn nhất, nhỏ nhất của hàm số thi ĐGNL HN
- Bài tập sự đồng biến, nghịch biến thi ĐGNL HN
