Trong không gian Oxyz, cho hai điểm A(−1;0;0) và B(2;3;4). Gọi (P) là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu (S1):(x−1)2+(y+1)2+z2=4 và (S2):x2+y2+z2+2y−2=0. Xét M,N là hai điểm bất kỳ thuộc mặt phẳng (P) sao cho MN=1. Giả trị nhỏ nhất của AM+BN bằng
Trả lời bởi giáo viên
Ta có:
{(x−1)2+(y+1)2+z2=4x2+y2+z2+2y−2=0⇔{x2+y2+z2−2x+2y−2=0x2+y2+z2+2y−2=0⇒x=0
Vậy (P):x=0((P) là mặt phẳng (Oyz)).
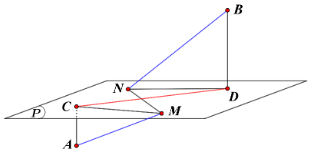
Gọi C(0;0;0) và D(0;3;4) lần lượt là hình chiếu vuông góc của A(−1;0;0), B(2;3;4) lên mặt phẳng (P). Suy ra AC=1,BD=2,CD=5.
Áp đụng bất đẳng thức √a2+b2+√c2+d2≥√(a+c)2+(b+d)2, ta được:
AM+BN=√AC2+CM2+√BD2+DN2≥√(AC+BD)2+(CM+DN)2≥√9+(CM+DN)2
Mặt khác, CM+MN+ND≥CD=5 suy ra CM+ND≥4. Do đó AM+BN≥5.
Dấu “=” xảy ra khi C,M,N,D thẳng hàng theo thứ tự đó và ACCM=BDDN, tức là M(0;45;1615) và N(0;75;2815).
Vậy giá trị nhỏ nhất của AM+BN là 5.
Hướng dẫn giải:
- Tìm mặt phẳng giao tuyến của (S1) và (S2)
- Gọi C và D lần lượt là hình chiếu vuông góc của A, B lên mặt phẳng (P). Tìm C, D.
- Áp đụng bất đẳng thức √a2+b2+√c2+d2≥√(a+c)2+(b+d)2 với a=AC,b=CM,c=BD,d=DN.
- Tìm điều kiện để dấu “=” xảy ra


