Hình chóp $S . A B C$ có đáy $A B C$ là tam giác vuông tại \(A,BC = 2a,ABC = {60^\circ }\). Gọi \(M\) là trung điểm cạnh \({\rm{BC}}\) và \({\rm{SA}} = {\rm{SC}} = {\rm{SM}} = {\rm{a}}\sqrt 5 \). Khoảng cách từ \({\rm{S}}\) đến cạnh \({\rm{AB}}\) là:

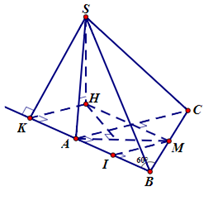
Chân đường cao hình chóp là tâm \({\rm{H}}\) của đường tròn ngoại tiếp tam giác \({\rm{AMC}}\) (Do \({\rm{SA}} = {\rm{SC}} = {\rm{SM}})\).

Góc \({\rm{AMC}} = {120^\circ }\), nên \({\rm{H}}\) ở ngoài tam giác \({\rm{AMC}}\) và \({\rm{HAM}}\) là tam giác đều nên:

\({\rm{HM}} = {\rm{AM}} = {\rm{a}}\)

\({\rm{SH}} = \sqrt {{\rm{S}}{{\rm{M}}^2} - {\rm{H}}{{\rm{M}}^2}} = \sqrt {5{{\rm{a}}^2} - {{\rm{a}}^2}} = 2{\rm{a}}\)

Từ \({\rm{H}}\) kẻ \({\rm{HK}} \bot {\rm{AB}}\) thì \({\rm{SK}} \bot {\rm{AB}} \Rightarrow {\rm{SK}}\) là khoảng cách từ \(S\) đến cạnh AB.

\({\rm{HK}} = {\rm{MI}} = \dfrac{{{\rm{a}}\sqrt 3 }}{2}\) (do \({\rm{ABM}}\) là tam giác đều cạnh bằng \({\rm{a}})\)

\({\rm{SK}} = \sqrt {{\rm{S}}{{\rm{H}}^2} + {\rm{H}}{{\rm{K}}^2}} = \sqrt {4{{\rm{a}}^2} + \dfrac{{3{{\rm{a}}^2}}}{4}} = \sqrt {\dfrac{{19{{\rm{a}}^2}}}{4}} = \dfrac{{{\rm{a}}\sqrt {19} }}{2}\)