Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với (ABCD) cà SA=a√6. Tính sin của góc tạo bởi AC và mặt phẳng (SBC).
Trả lời bởi giáo viên
Đáp án đúng: d
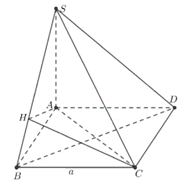
Kẻ AH⊥SB⇒BC⊥AH⇒AH⊥(SBC)
⇒AH là hình chiếu của AC lên mặt phẳng (SBC)⇒(^AC,(SBC))=(^AC,HC)=^ACH.
Tam giác SAB vuông ⇒AH=SA⋅ABSB=a√6⋅aa√7=a√6√7
Vì vuông tại H⇒sin^ACH=AHAC=√3√7.
Hướng dẫn giải:
Kẻ AH⊥SB⇒BC⊥AH⇒AH⊥(SBC).
Từ đó xác định góc tạo bởi AC và mặt phẳng (SBC).


