Cho tứ diện \({\rm{ABCD}}\). Điểm \({\rm{M}}\) thuộc đoạn \({\rm{AC}}\) ( \({\rm{M}}\) khác \({\rm{A}},{\rm{M}}\) khác \({\rm{C}}\) ). Mặt phẳng \((\alpha )\) đi qua \({\rm{M}}\) song song với \({\rm{AB}}\) và \({\rm{AD}}\). Thiết diện của \((\alpha )\) với tứ diện \({\rm{ABCD}}\) là hình gì?
Trả lời bởi giáo viên
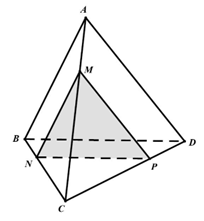
Ta có \(\left. {\begin{array}{*{20}{l}}{(\alpha )//{\rm{AB}}}\\{{\rm{AB}} \subset ({\rm{ABC}})}\end{array}} \right\} \Rightarrow (\alpha ) \cap ({\rm{ABC}}) = {\rm{MN}}\)
Với \(MN//AB\) và \(N \in BC\).
Ta có \(\left. {\begin{array}{*{20}{l}}{(\alpha )//{\rm{AD}}}\\{{\rm{AD}} \subset ({\rm{ADC}})}\end{array}} \right\} \Rightarrow (\alpha ) \cap ({\rm{ADC}}) = {\rm{MP}}\)
Với \({\rm{MP}}//{\rm{AD}}\) và \({\rm{P}} \in {\rm{CD}}; (\alpha ) \cap ({\rm{BCD}}) = {\rm{NP}}.\)
Do đó thiết diện của \((\alpha )\) với tứ diện \({\rm{ABCD}}\) là hình tam giác MNP .
Hướng dẫn giải:
Tìm giao tuyến của các cặp mặt phẳng: \((\alpha ) \cap ({\rm{ABC}})\) và \((\alpha ) \cap ({\rm{ADC}})\)


