Câu hỏi:
1 năm trước
Tìm $m$ để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \)
Trả lời bởi giáo viên
Đáp án đúng: c
+) TH1: \( - 1 \le m - 1 \le 1 \Leftrightarrow 0 \le m \le 2\)
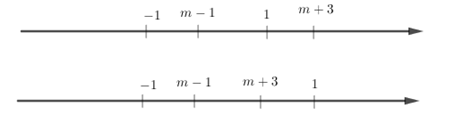
+) TH2: \(m - 1 \le - 1 \le m + 3 \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 4\end{array} \right. \Leftrightarrow - 4 \le m \le 0\)
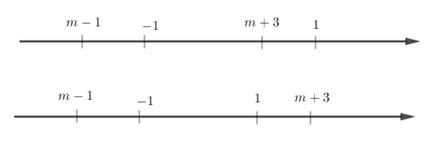
Kết hợp hai trường hợp trên ta được \(\left[ \begin{array}{l} 0 \le m \le 2\\ - 4 \le m \le 0\end{array} \right. \Leftrightarrow - 4 \le m \le 2\)
Hướng dẫn giải:
Liệt kê các trường hợp để hai tập hợp \(\left[ { - 1;1} \right]\) và \(\left[ {m - 1;m + 3} \right]\) có giao khác rỗng (biểu thị trên trục số).
Giải thích thêm:
Cách giải trên thuận tiện cho việc biện luận phần giao của hai tập hợp, còn trong bài toán này, các em có thể giải bài toán bằng phương pháp phần bù như sau:
Tìm \(m\) để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] = \emptyset \Leftrightarrow \left[ \begin{array}{l}1 < m - 1\\m + 3 < - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 4\end{array} \right. \Leftrightarrow m \in \left( { - \infty ; - 4} \right) \cup \left( {2; + \infty } \right) = A\)
Khi đó để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \) thì \(m \in R\backslash A = \left[ { - 4;2} \right]\) hay \( - 4 \le m \le 2\).
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 3 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 4 Toán 10 sách Cánh diều có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 10 sách Cánh diều có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 10 sách Cánh diều có lời giải chi tiết
