Câu hỏi:
2 năm trước
Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình $\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) > 0$ là
Trả lời bởi giáo viên
Đáp án đúng: a
Bất phương trình $\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) > 0 \Leftrightarrow 3{\left( {x - 2} \right)^2}\left( {x + 2} \right)\left( {x - 1} \right) > 0$
Vì ${\left( {x - 2} \right)^2} > 0,\,\,\forall x \ne 2$ nên bất phương trình trở thành $\left\{ \begin{array}{l}x \ne 2\\\left( {x + 2} \right)\left( {x - 1} \right) > 0\end{array} \right..$
Đặt $f\left( x \right) = \left( {x + 2} \right)\left( {x - 1} \right).$
Phương trình $x + 2 = 0 \Leftrightarrow x = - \,2$ và $x - 1 = 0 \Leftrightarrow x = 1.$
Ta có bảng xét dấu
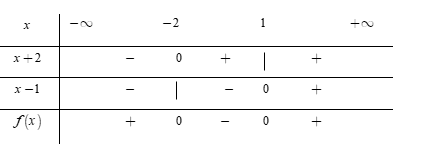
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0$$ \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1; + \,\infty } \right).$
Kết hợp với điều kiện $x \ne 2,$ ta được $ \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1;2} \right) \cup \left( {2; + \,\infty } \right).$
Do đó, nghiệm nguyên âm lớn nhất của bất phương trình là $ - \,3$ và nghiệm nguyên dương nhỏ nhất của bất phương trình là $3.$
Vậy tích cần tính là $\left( { - \,3} \right).3 = - \,9.$
Hướng dẫn giải:
- Giải bất phương trình đã cho bằng việc xét dấu các nhị thức bậc nhất có trong vế trái.
- Tìm tập nghiệm của bất phương trình suy ra nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất và kết luận.
Giải thích thêm:
Cần chú ý đến điều kiện \(x \ne 2\) khi xét dấu \(f\left( x \right) = \left( {x + 2} \right)\left( {x - 1} \right)\). Nhiều em quên mất điều kiện đó dẫn đến tìm sai tập nghiệm và chọn nhầm đáp án B là sai.
