Câu hỏi:
2 năm trước
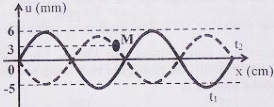
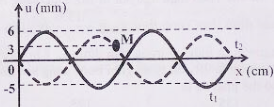
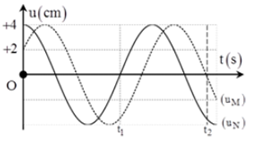
Sóng ngang có tần số \(f\) truyền trên một sợi dây đàn hồi rất dài, với tốc độ \(3m/s\). Xét hai điểm M và N nằm trên cùng một phương truyền sóng, cách nhau một khoảng \(x\). Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian \(t\) như hình vẽ. Biết \({t_1} = 0,05s\). Tại thời điểm \({t_2}\), khoảng cách giữa hai phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
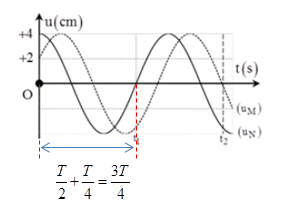
+ Từ đồ thị ta thấy:
- Khoảng thời gian \({t_1} = \frac{{3T}}{4} = 0,05s \to T = \frac{1}{{15}}s\)
Tần số góc: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{1}{{15}}}} = 30\pi \left( {rad/s} \right)\)
- Bước sóng: \(\lambda = vT = 3.\frac{1}{{15}} = 0,2m = 20cm\)
Từ đồ thị ta suy ra phương trình sóng tại M và N
- PTDĐ tại M: \({u_M} = A\cos \omega (t - \frac{{{d_1}}}{v})\)
\({u_M} = 4\cos (30\pi t - \frac{\pi }{3})cm\)
- PTDĐ tại N: .\(\)\({u_N} = 4\cos (30\pi t)cm\)
Độ lệch pha giữa hai sóng: \(\Delta \varphi = \frac{\pi }{3} - 0 = \frac{\pi }{3} = \frac{{2\pi x}}{\lambda } \to x = \frac{\lambda }{6} = \frac{{20}}{6} = \frac{{10}}{3}cm\)
+ Tại \(t = {t_2} = \frac{T}{6} + \frac{T}{4} + T = \frac{{17T}}{{12}} = \frac{{17}}{{12}}.\frac{1}{{15}} = \frac{{17}}{{180}}s\) (N đi từ \(\frac{A}{2}\left( { + 2} \right) \to A\left( { + 4} \right) \to 0\) rồi đi thêm 1 chu kì nữa):
\(\begin{array}{l}{u_M} = 0cm\\{u_M} = 4\cos (30\pi {t_2}) = 4cos\left( {30\pi .\frac{{17}}{{180}}} \right) = 4cos\left( {\frac{{11\pi }}{6}} \right) = - 2\sqrt 3 cm\end{array}\)
Khoảng cách giữa hai phần tử M và N tại \({t_2}\) là:
\(d = \sqrt {{x^2} + \Delta {u^2}} = \sqrt {{{\left( {\frac{{10}}{3}} \right)}^2} + {{\left( {0 - \left( { - 2\sqrt 3 } \right)} \right)}^2}} = \frac{{4\sqrt {13} }}{3} \approx 4,81cm\)
Hướng dẫn giải:
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Viết phương trình dao động sóng
+ Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {{x^2} + \Delta {u^2}} \)
Câu hỏi khác
- Bài tập các đại lượng đặc trưng của sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập lí thuyết về sóng cơ và sự truyền sóng cơ có đáp án MÔN LÝ lớp 12
- Bài tập lý thuyết chung về giao thoa sóng có lời giải MÔN LÝ lớp 12
- Bài tập phương trình sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập đồ thị sóng cơ học có đáp án MÔN LÝ lớp 12
