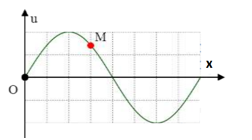
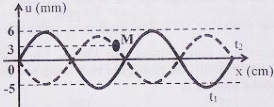
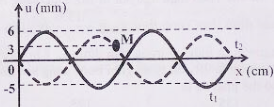
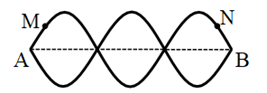
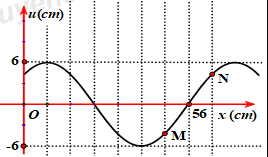
Một sóng hình sin lan truyền trên một sợi dây đàn hồi theo chiều từ \(M\) đến \(O.\) Hình vẽ bên mô tả hình dạng của sợi dây tại thời điểm\({t_1}\). Cho tốc độ truyền sóng trên dây bằng \(64 cm/s.\) Vận tốc của điểm \(N\) tại thời điểm \({t_2} = {t_1} + \dfrac{1}{3}\,s\) gần đúng với giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Từ đồ thị ta thấy \(7\) ô tương ứng với \(56cm,\) vậy \(1\) ô tương ứng với \(8cm.\)
Một bước sóng tương ứng với \(8\) ô. Vậy: \(\lambda = 8.8 = 64cm\)
Có \(v = 64cm \Rightarrow T = \dfrac{\lambda }{v} = \dfrac{{64}}{{64}} = 1s \Rightarrow \omega = 2\pi rad/s\)
Khoảng cách \(MN\) theo phương truyền sóng tương ứng \(2\) ô nên độ lệch pha của \(M\) và \(N\) là:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi .\dfrac{\lambda }{4}}}{\lambda } = \dfrac{\pi }{2}\)
Góc quét được sau \(\dfrac{1}{3}s\) là:
\(\alpha = \omega .\Delta t = 2\pi .\dfrac{1}{3} = \dfrac{{2\pi }}{3}rad = {120^0}\)
Biểu diễn \(M\) và \(N\) tại \(t_1\) và \(t_2\)trên VTLG:
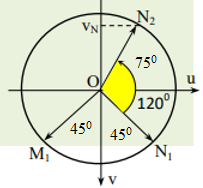
Từ VTLG ta có:
\({v_N}\left( {{t_2}} \right) = - A\omega .\sin 75 = - 6.2\pi .\sin 75 = - 36,41cm/s\)
Hướng dẫn giải:
Độ lệch pha giữa \(M\) và \(N:\) \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Sử dụng kĩ năng đọc đồ thị và VTLG.