Số vị trí biểu diễn các nghiệm của phương trình \(4{\sin ^2}x - 4\sin x - 3 = 0\) trên đường tròn lượng giác là:
Trả lời bởi giáo viên
\(4{\sin ^2}x - 4\sin x - 3 = 0\)
Đặt \(\sin x = t\,\,\left( { - 1 \le t \le 1} \right)\) khi đó phương trình có dạng: \(4{t^2} - 4t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{3}{2}\,\,\,\,\,\,\left( {ktm} \right)\\t = - \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right.\)
\(t = - \dfrac{1}{2} \Leftrightarrow \sin x = - \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)\)
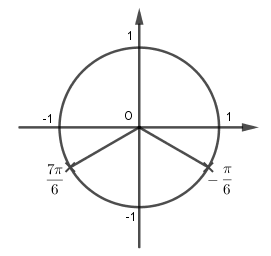
Vây số vị trí biểu diễn các nghiệm của phương trình \(4{\sin ^2}x - 4\sin x - 3 = 0\) trên đường tròn lượng giác là 2 điểm như hình trên.
Hướng dẫn giải:
- Giải phương trình bậc hai đối với \(\sin x\) tìm nghiệm.
- Biểu diễn các nghiệm trên đường tròn đơn vị và kết luận.

