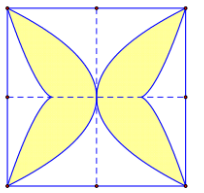
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh \(40\,\left( {cm} \right)\) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình \(4{x^2} = {y^4}\) và \(4{\left( {\left| x \right| - 1} \right)^3} = {y^2}\) để tạo hoa văn cho viên gạch. Diện tích phần được tô đậm gần nhất với giá trị nào dưới đây?
Trả lời bởi giáo viên
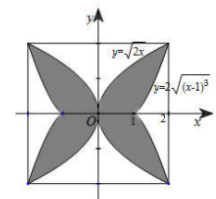
Gắn hệ trục tọa độ như hình vẽ.
Diện tích phần tô đậm là \(S = 4\left[ {\int\limits_0^1 {\left( {\sqrt {2x} - 0} \right)dx} + \int\limits_1^2 {\left( {\sqrt {2x} - 2\sqrt {{{\left( {x - 1} \right)}^3}} } \right)dx} } \right] = \dfrac{{112}}{{15}}\,\,\left( {d{m^2}} \right) \approx 747\,\,\left( {c{m^2}} \right)\).
Hướng dẫn giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).