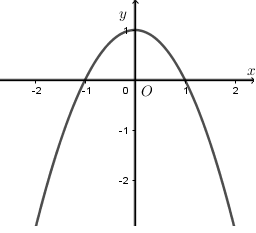
Gọi $S$ là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ ($S$ được giới hạn bởi parabol $\left( P \right)$ và trục $Ox$). Giá trị của S là:
Trả lời bởi giáo viên
Gọi phương trình parabol: $y=ax^2+bx+c (a\ne 0)$
Parabol có đỉnh $(0;1)$ nên $c=1$ và $-\dfrac{b}{2a}=0$ hay $b=0$.
Do đó $y=ax^2+1$.
Lại có các điểm $(-1;0),(1;0)$ thuộc đồ thị hàm số nên $a.1^2+1=0\Leftrightarrow a=-1$
Ta thấy, phương trình đường cong parabol trong hình là: \(y = - {x^2} + 1\)
$ \Rightarrow S = \int_{ - 1}^1 {\left| {1 - {x^2}} \right|dx} = \left. {\left( {x - \dfrac{1}{3}{x^3}} \right)} \right|_{ - 1}^1 = \dfrac{4}{3}$
Hướng dẫn giải:
+ Từ đồ thị tìm ra được phương trình đường cong parabol.
+ Tính diện tích phần hình giới hạn bởi parabol và trục hoành:
- Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\)
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)

