Câu hỏi:
3 năm trước
Một vật thể tròn xoay sinh ra bởi phép quay xung quanh trục $O x$ của hình giới hạn bởi trục $O x$ và đường \(y = \sin x,(0 \le x \le \pi )\) như hình vẽ:
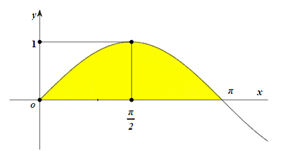
Tính thể tích vật thể.
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(V = \pi \int\limits_0^\pi {{{\sin }^2}xdx} = \pi \int\limits_0^\pi {\dfrac{{1 - \cos 2x}}{2}dx} = \left. {\dfrac{\pi }{2}\left( {x - \dfrac{{\sin 2x}}{2}} \right)} \right|_0^\pi = \dfrac{{{\pi ^2}}}{2}\).
Hướng dẫn giải:
Thể tích vật thể tròn xoay sinh ra được tính bởi công thức: \(V = \pi \int_0^\pi {{{\sin }^2}} xdx\)


