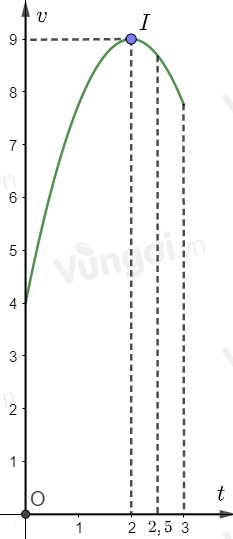
Một vật chuyển động trong 3 giờ với vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\) có đồ thị là một phần của parabol có đỉnh \(I\left( {2;\,\,9} \right)\) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?
Trả lời bởi giáo viên
Vì vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\) có đồ thị là một phần của parabol nên ta có hàm số \(v =f(t)= a{t^2} + bt + c\,\,\,\left( {a \ne 0} \right)\).
Dựa vào đồ thị hàm số ta có: tại thời điểm \(t = 0\), \(v = 4\)\(\Rightarrow a.0^2+b.0+c=4 \Rightarrow c = 4\)
Đồ thị hàm số có đỉnh \(I\left( {2;9} \right)\)\( \Rightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{{2a}} = 2\\f\left( 2 \right) = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a{.2^2} + b.2 + 4 = 9\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b = 5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{ - 5}}{4}\\b = 5\end{array} \right.\)
\( \Rightarrow v = - \dfrac{5}{4}{t^2} + 5t + 4\)
Tại lúc 2 giờ 30 phút = 2,5 giờ vận tốc đạt được là:
\(v\left( {2,5} \right) = \dfrac{{ - 5}}{4}.2,{5^2} + 5.2,5 + 4\)\( = 8,6875\,\,\left( {km/h} \right) \approx 8,7\,\,\left( {km/h} \right)\)
Hướng dẫn giải:
Chuyển bài toán thực tế về dạng toán tìm hệ số \(a,\,\,b,\,\,c\) của hàm số bậc hai \(y = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right)\) vì vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc thời gian \(t\,\,\left( h \right)\) có đồ thị là một phần của parabol.


