Câu hỏi:
2 năm trước
Một tia sáng được chiếu đến điểm chính giữa của mặt trên một khối lập phương trong suốt, chiết suất n = 1,5. Xác định góc tới lớn nhất để tia khúc xạ còn gặp mặt đáy của khối lập phương?
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi độ dài cạnh hình lập phương là a
Theo định luật khúc xạ ánh sáng, ta có: \(1.\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}}\)
Khi imax thì rmax
Ta có, rmax khi tia khúc xạ đến một đỉnh ở đáy của khối lập phương.
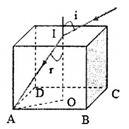
Từ hình vẽ, ta có:
\({\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = \frac{{OA}}{{AI}} = \frac{{0,5{\rm{a}}\sqrt 2 }}{{\sqrt {{a^2} + {{(0,5{\rm{a}}\sqrt 2 )}^2}} }} = \frac{1}{{\sqrt 3 }}\)
\( \to \sin {i_{{\rm{max}}}} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = 1,5.\frac{1}{{\sqrt 3 }} \to {i_{{\rm{max}}}} = {60^0}\)
Hướng dẫn giải:
+ Vẽ đường truyền của tia sáng trong khối lập phương
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
+ Sử dụng hệ thức lượng giác
