Câu hỏi:
2 năm trước
Một thợ lặn dưới nước nhìn thấy Mặt Trời ở độ cao \({50^0}\) so với đường chân trời. Độ cao thực của Mặt Trời (tạo một góc bao nhiêu độ so với đường chân trời) là bao nhiêu? Biết chiết suất của nước là \(\dfrac{4}{3}\)
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có:
+ Góc tạo bởi Mặt Trời và phương ngang chính là góc của Mặt Trời so với đường chân trời
+ Vẽ hình ta được:
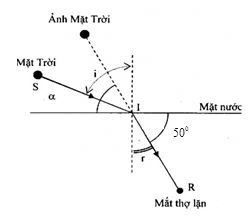
Từ hình, ta suy ra: Góc khúc xạ \(r = {90^0} - {50^0} = {40^0}\)
+ Vận dụng định luật khúc xạ, ta có:
\(\begin{array}{l}\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Leftrightarrow \sin i = \dfrac{4}{3}\sin {40^0}\\ \Rightarrow \sin i = 0,857 \to i \approx {59^0}\end{array}\)
+ Góc mà Mặt Trời tạo với đường chân trời là: \(\alpha = {90^0} - {59^0} \approx {31^0}\)
Hướng dẫn giải:
+ Dựng ảnh của vật bằng hiện tượng khúc xạ ánh sáng
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
